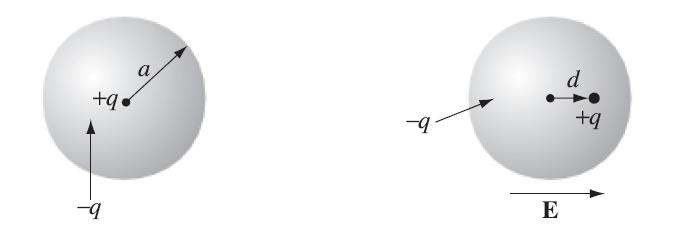版权声明 :
本文采用 CC BY-NC-SA 4.0
许可信息:
严禁将本文内容用于商业用途。更多许可政策详情,请访问 关于 页面。
1. 矢量代数 我们将忽略非常简单的运算。
1.1 三重积:
1.2 Nabla 算符:
对于单位矢量,
微分意味着当
增加一个无穷小量时,
如何变化。
即:
笛卡尔坐标系:
球坐标系:
其他项同理。
基于这些表格,我们可以导出:
梯度:
散度:
总结:
1.3 Nabla 算符的性质
证明:
由于
是解析函数,
混合偏导数相等。
因此
。
证明:
证明:仅考虑一个分量(其他分量循环对称)。
对其他分量进行同样操作并组合在一起,得证。
证明:仅考虑一个分量(其他分量循环对称)。
对其他分量进行同样操作并组合在一起,得证。
证明:
我们有矢量三重积公式:
。
将这些矢量替换为
和
。
我们需要解释为什么 微分算符需要作用于函数。nabla 算符总是作用于其右侧的函数。
证明:
类似于此过程:
同理:
证明:
因为
则
分别化简这四项:
最终
证明:
同理。
最后去掉所有的
并合并
和
的结果。
公式得证。
请注意,这里的
证明:
证明:
证明:
分量为
取散度
组合在一起,则
1.4 并项张量(Dyadic Tensor)
这实际上是张量积。最终空间为
结果是一个二阶张量。
分量解释:
1.5 Levi-Civita 符号
或 或 或 或 偶 置 换 或 或 奇 置 换
那么
1.6 两个定理 定理: 如果
证明:
假设
定理: 如果
证明:
1.7 应用实例 这里提供一些应用实例:
因为
那么
因为
那么
由于
那么
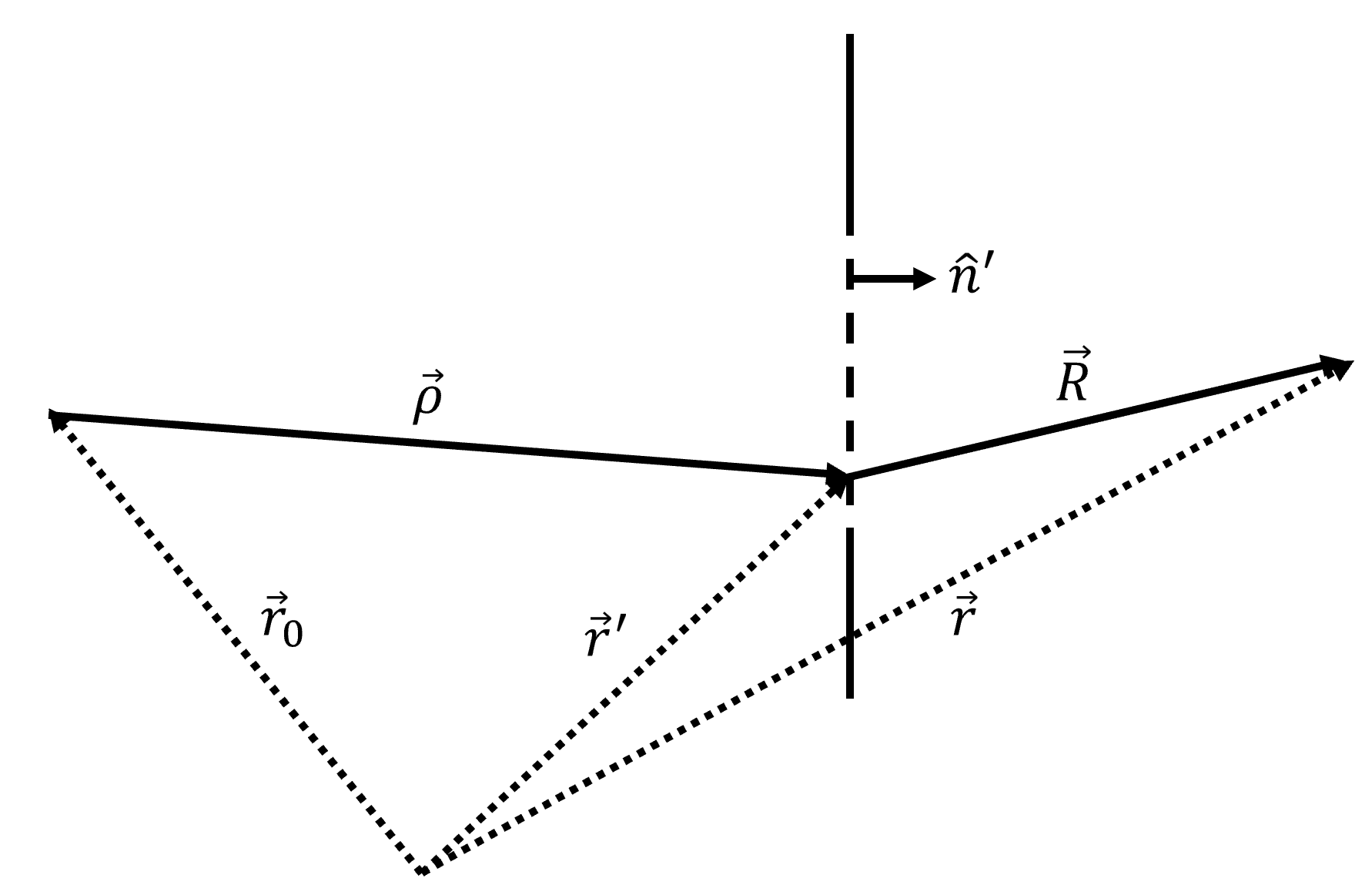
2. 静电场 2.1 场与电势
注意
是观测点的绝对位置,而
是电荷的位置。
上述公式可以写成更紧凑的形式:
其中
被定义为电势 (Electric Potential),它是一个标量势场 。
注意
算符不对
作用,因为
是对观测空间坐标求导。对于微元场:
此处
是一个常矢量(固定电荷位置)。
接下来我们可以计算旋度和散度:
取一个包含
的任意体积:
在
处,
,但其积分值是有限的。因此
。
最后我们得到:
根据上述推导,我们可以得出一些重要结论:
静态场的 Poisson 方程 :
静电场是有源无旋场。
此外,还有 Earnshaw 定理 。
Earnshaw 定理 :点电荷在静电场中无法处于稳定的平衡状态。
证明:稳定平衡
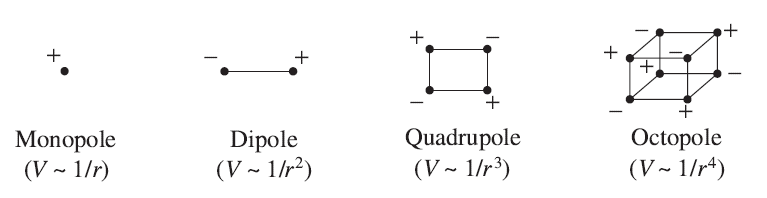
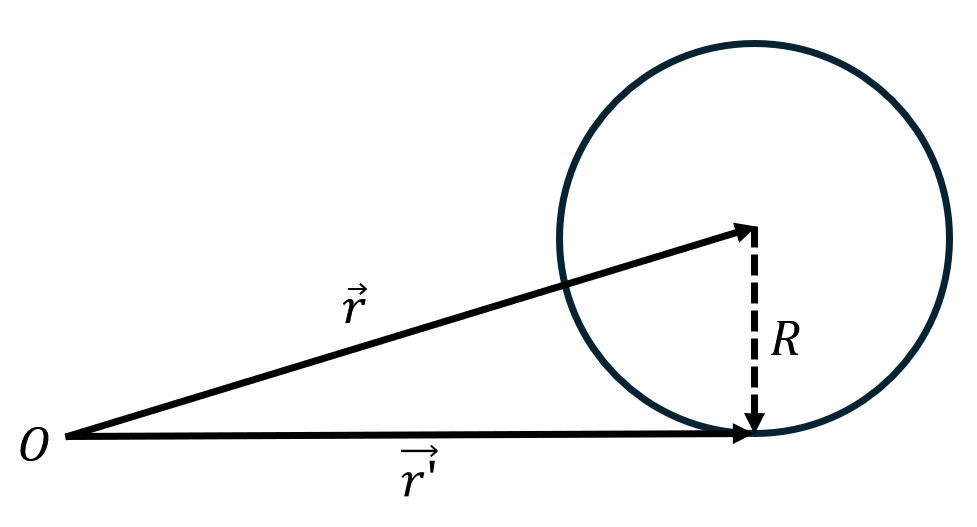
2.2 多极展开(Multipole Expansion) 当你距离局部电荷分布非常遥远时,如果总电荷
不同的多极子
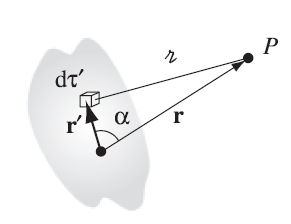
现在我们推导多极子的电势。在某点
利用余弦定理:
定义
电荷分布产生的场
应用 Taylor 展开 :
将
巧合的是,Legendre 多项式 。我们得出结论:
上述展开中的各项代表了不同多极子的贡献。
项是单极子贡献。
项是偶极子,
是四极子,
是八极子,等等。
通常情况下,展开式由单极子项主导,即点电荷。
如果
,则主导项将是偶极子项:
我们定义:
为电偶极矩 。偶极贡献简化为:
通常,如果你移动坐标原点,
偶极子的电场为:
此外,我们还可以提取四极子的贡献:
这两项积分可以合并为一个项:
四极矩张量 定义为:
显而易见
很容易验证
此外,为了获得更紧凑的形式,可以使用 Taylor 展开 的紧凑形式来展开
在静电势中:
四极子的贡献:
对于算符部分:
将此项代入
其中
四极子产生的电场为:
考虑
首先计算二次型的梯度:
对 称 性 然后得到:
如果一个四极子被放置在外电场
对于纯四极子,其单极矩(总电荷)和偶极矩均为 0。因此只剩下一项:
回顾使用 Legendre 多项式 的电势展开:
**Legendre 多项式**可以进一步用球谐函数(spherical harmonics)展开:
将展开式代入电势并重新排列:
由此可以定义多极矩分量:
它是
-极矩张量
的元素。
2.3 静电场的唯一性定理(Uniqueness Theorem)
假设一个静态系统由多个均匀介质或导体区域组成。
已知电荷分布
,
各导体的总电荷
或电势
,
以及边界上的电势
或其沿法向的导数
,
那么场分布是唯一的。
这就是唯一性定理 。
证明:
假设存在两个电势解:
和
。
考虑两个相邻区域
。
我们有:
以及对于
的相同方程组。
定义差值电势:
则差值电势满足:
无 源 方 程
考虑由差值电势定义的能量项:
同时:
由于满足 **Poisson 方程**,第二项消失。
于是:
现在考虑两种边界条件:
1. 如果给定边界上的电势
,则
,故
;
2. 如果给定法向导数
,则
,故
。
定理得证。
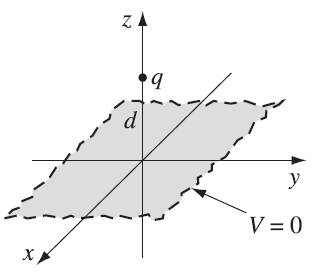
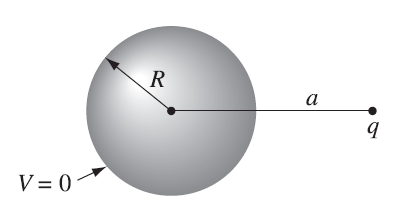
2.4 镜像法(Method of Image) 假设一个点电荷
初始配置
系统满足两个边界条件:
基于唯一性定理,只要
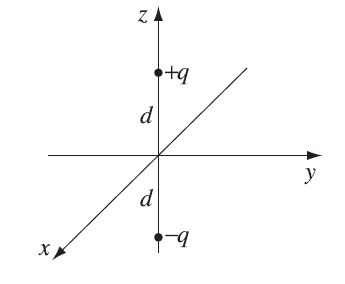
为了简化,我们可以用另一种配置来达到相同的边界条件:
新配置
在 镜像电荷 。在此配置下,
该电势在
感应电荷密度
受力为:
系统能量为:
简而言之,镜像法的核心是唯一性定理。
另一个例子:
应用于球体的镜像法
我们尝试用
为了满足边界条件
计算得到:
电势分布为:
受力为:
2.5 Green 函数法(Green Function Method)
这种方法在实际应用中比镜像法更强大。
考虑一般性问题,电势满足 Poisson 方程:
首先介绍 **Green 第二公式**:
我们得到 **Poisson 公式**:
这种方法的局限性在于:要求同时知道边界上的电势和梯度。
代入公式得到:
这是 Poisson 方程 可解性的必要条件。
平均值定理(Mean Value Theorem) :
球心处的电势等于球面上电势的平均值
对于特定的边界条件:
Dirichlet 边界条件 (给定边界电势):
其中 Green 函数 ,在边界上
Neumann 边界条件 (给定边界法向导数):
其中
3. 静磁场 3.1 场与电势 为了展示电流的方向,我们可以定义电流密度
则有
存在一个实验定律:Biot - Savart 定律。
Biot - Savart 定律: 对于两个电流元 其 中
进一步将
写成紧凑形式:
不 对 作 用
类似于电场,我们可以为磁场定义一个势
。但
是一个矢量。
进一步考察
:
对于任何函数
,
因此
对于第一项,因为
该项包含了整个空间,所以我们可以取一个
的球面。
由于
在无穷远处趋于 0,第一项坍缩为 0。
同时
对于第二项:
最后:
3.2 Lorentz 力
在所有惯性系下,Lorentz 力具有相同的形式。
对于电流
通常情况下,电流密度
与单位电荷受力成正比:
是 Lorentz 力(2.3 中提到过)。
代入受力公式:
通常电荷的速度足够小,磁场项可以忽略。
其中
称为电导率。该公式被称为 Ohm 定律。
这可能令人困惑,因为我们知道导体内部的电场为 0。但金属导线内部是有电流的,这似乎违反了 Ohm 定律。然而,这一结论只是一个近似。导体的
非常大,以至于只需极小的电场就能驱动巨大的电流。因此在大多数情况下,即使电荷在移动,内部电场也可以被忽略。
3.3 磁场的多极展开 类似于电场,磁矢势也可以用 Legendre 多项式展开:
与电展开不同的是,单极子项
消失了,因为
。
这一结果表明磁场没有单极子,
这与以下预测一致:
在没有任何单极子贡献的情况下,主导项是偶极子项:
根据 Stokes 公式:
设
,其中
是一个常矢量。
因此
代入
,
最终得到磁偶极子的势:
其中磁偶极矩
定义为
磁偶极子产生的磁场为:
上述证明是针对小型、细环形电流的特殊情况。
在一般情况下,
被替换为
。
当磁偶极子被置于外磁场中时,
其受到的总力为:
第一项始终为零,因为没有电流进出该体积。
忽略高阶项后,
考虑一个 3 阶张量
及其散度:
由于表面电流为零且
,
我们有
此外对于
:
利用下式的反向形式:
我们可以发现
对于偶极子,
是一个常矢量。
所以
同样地,无电流变化导致
。
通过
,
能量也就很明确了:
需要澄清的是,
磁效应比电效应弱得多。
磁偶极子的效应接近于电四极子。
因此,
在大多数情况下我们只关注磁偶极子,忽略高阶效应,
包括磁四极子(其影响接近于电八极子)。
3.4 静磁场的唯一性定理 类似于电学,磁场也有唯一性定理。
假设系统
内部有恒定电流,
。
如果电流分布、物质分布以及
或
的切向分量已知,
那么系统中的
就能被唯一确定。
证明过程也类似。
假设
满足所有条件。
由此可知
或
定义差值量:
显而易见
或
我们得到差值场的能量
差值场不包含能量,
意味着各处
。
证毕。
4. 变化场 4.1 随时间变化的电场
Faraday 发现
的变化会产生电动势。
其中
是磁通量。
我们可以推导出其微分形式。
消去积分符号
,我们得到:
4.2 随时间变化的磁场
如果我们考虑到
的变化,会发现一个冲突。
但对等式两边取散度:
这意味着
,但在物理学中这并非必然。电荷守恒定律表明:
为了消除这个冲突,我们需要引入一个新项。
新 项 新 项
根据:
则有:
4.3 真空中的 Maxwell 方程组 根据上述推导,我们可以总结出 Maxwell 方程组:
注意在最后的积分形式中,
项通常被写为
,
其中
是电位移场。
类似地,
磁场积分方程有时使用磁场强度
而非
来表示,
在真空中
。
上图展示了使用
的形式。
4.4 Maxwell 方程组的完备性 完备性:给定初始条件和边界条件,
证明。给定初始条件:
边界条件:
定义:
则有:
根据 Maxwell 方程组:
定义:
则:
由 于 边 界 条 件
结合初始条件可知,
。因此
。
5. 介质中的场 5.1 极化 具有相等正负电荷(总体中性)的物体称为偶极子。当偶极子置于
偶极子的偶极矩为:
称为极化率,取决于偶极子的结构。
如果正负电荷之间的距离为
的方向是从负电荷指向正电荷。以极化原子为例:
极化原子
由负电荷产生的场为:
正电荷在平衡状态下保持静止。因此:
因此极化率为:
对于更复杂的分子,
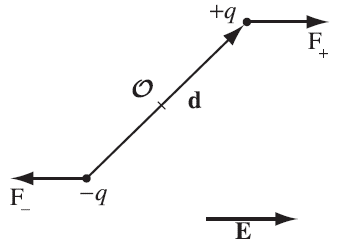
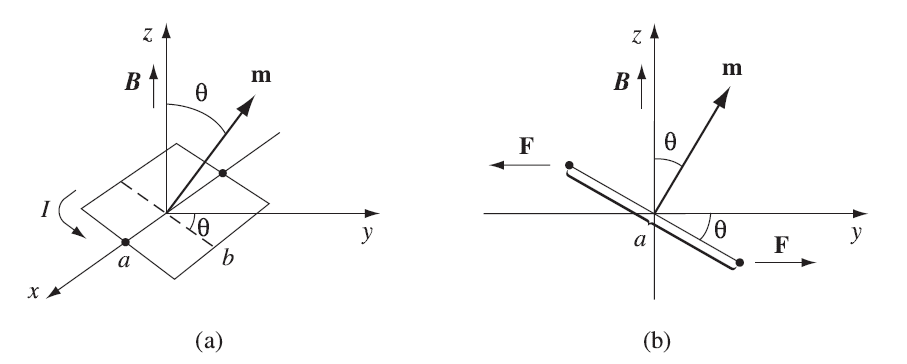
外场产生的力矩为:
在均匀场中(或者当
非常小时):
偶极子受力
在非均匀场中,假设
则非均匀场中的力矩为:
偶极子在电场
在均匀场中:
5.2 偶极子的电势和力 现在讨论偶极子产生的场。
其电势为:
且:
使用 Taylor 级数展开(对于
忽略二阶项:
则有:
以及电场:
示例: 两个相互作用的偶极子
考虑
,
5.3 宏观极化 如果一个物体包含许多偶极子,定义
电势变为:
其中
对其重新整理:
这两项分别是面电荷和体电荷产生的电势。因此:
表 面 体 积 我们之前没有考虑任何自由电荷。上述所有电荷都是由极化产生的。它们被束缚在物体内,不能自由移动。此类电荷被称为束缚电荷。
5.4 电位移 我们现在将自由电荷考虑在内。
根据 Gauss 定律:
为了方便,定义:
为电位移矢量,那么 Gauss 定律可以简化为:
积分形式为:
对于旋度(先忽略
对于许多物质,
则有:
从另一个视角看,介电常数随物质改变:
如果物质不是各向同性的,
能量应为:
5.5 磁化 所有磁现象都归因于运动的电荷。与电极化类似,当施加磁场时,磁偶极子(由极化原子产生)会产生净排列,随后介质被磁化。
磁化方向并不总是与外部
磁偶极子是一个微小的电流环路。最简单的例子是矩形偶极子。
矩形磁偶极子
在 z 方向均匀磁场中的力矩为:
其中
相邻边总是具有相反的电流,因此它们相互抵消。
靠近边缘的边组成了原始的电流环路。力矩可以展开为:
非矩形偶极子
其中
对于磁场
那么对于宏观电流:
对于均匀磁场中的电流环路:
在非均匀磁场中,假设一个半径为
因此能量为:
此外,这还涉及偶极子的磁场和扰动。
对于电流密度
在一个偶极子中,
由于
以及磁场:
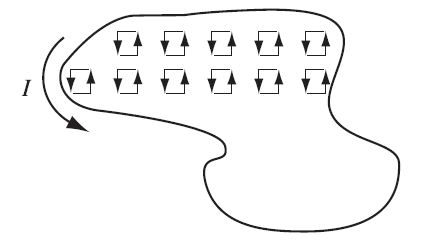
5.6 宏观磁化 对于物体,定义:
为总磁化强度。利用
(根据公式
第一项看起来像是体积效应:
第二项看起来像是表面效应:
则有:
和
分别是体积和表面的束缚电流。
现在考虑自由电流:
根据 Ampere 定律:
定义:
作为辅助场,则有:
积分形式为:
散度为:
仅当
与电场类似,
则有:
称为磁导率,
称为磁化率。
当物质不是各向同性时,
总是被展开为一个张量:
5.7 介质中的 Maxwell 方程组 我们首先列出真空中的 Maxwell 方程组:
在介质中,
和
被替换为
和
。
根据第 5 章和第 6 章,
Gauss 定律被替换为:
Ampere 环路定律被替换为:
5.8 边界条件 在不同物质的边界处,
取一个跨越边界的小圆柱体,底面积为
以及
并且:
取一个跨越边界的无限小宽度
根据 Faraday 定理:
则有
根据 Ampere 环路定律:
得出:
最后
6. 能量 6.1 电场能量
首先,我们研究离散电荷的情况。对于 2 个电荷,将
从无穷远处移至距离
为
的位置(设
为原点)所做的功为:
引入更多电荷:
最终所做的总功应为所有功之和:
去除重复项:
当离散电荷变为连续分布时:
其中
是场点,
是场源的位置。
应用 Maxwell 方程:
因此:
已知
,则:
我们在全空间进行积分,且在无穷远处
。
所以第一项:
最终得到:
6.2 磁场能量
假设有两个静止的回路。
在回路 1 中通以恒定电流
,
它会产生磁场
。
Biot-Savart 定律给出:
磁场与电流
成正比。
回路 2 的磁通量亦然:
称为回路 1 对回路 2 的互感。
现在带入磁矢势:
提取
:
我们可以发现一个惊人的结果:
的公式关于
和
是对称的。
因此,我们可以说:
我们随后去掉下标,统称为
。
利用电感,
根据 Faraday 定律,
回路 1 产生的磁场会在回路 2 中产生电动势:
此外,
回路 1 中的电流变化不仅在回路 2 中产生电动势,
在回路 1 自身也会产生电动势。
同样,它也与电流成正比:
这个新系数
称为自感。
在电感器中,电动势可以表示为:
单位时间内所做的总功为:
所以:
进一步推导:
因此:
根据 Maxwell 方程:
此 处 无
所以:
类似地,由于在无穷远处
:
6.3 Poynting 定理与能量守恒 从 Maxwell 方程组中提取两个方程:
进行如下乘法运算:
相减得:
重新整理该方程,我们得到:
我们定义:
为电磁场(EMF)的能量密度 。并将:
定义为 Poynting 矢量 ,代表能量流密度 。
项也可以表示如下:
因此 Poynting 定理也可以通过力密度
能 量 流 出 所 做 的 功 能 量 减 少
6.4 介质中的能量流 在介质中,重复上述过程,但将介电常数和磁导率替换为介质中的形式:
进行如下乘法运算:
相减得:
重新整理得到:
这就是介质形式的 Poynting 定理。Poynting 矢量为:
能量密度为:
7. 动量 7.1 Maxwell 应力张量
我们已知力密度为:
总力为:
我们提议仅用场来表示它。
为了简化
,引入 Maxwell 应力张量
:
由 于 因此:
其分量为:
力密度随后简化为:
通过积分得到总力:
7.2 动量守恒
我们用
表示机械动量。
在孤立空间中:
这是一个标准的守恒函数形式。
(密度的变化 = 流出体积的通量)
因此,该项:
一定也代表动量。
它由 EMF 携带。定义:
为 EMF 动量密度。
于是我们得到:
该方程即为 EMF 的动量守恒定律。
利用
的表示,我们将方程改写为无限小时间
内的积分形式:
左手边是单位时间内总动量的变化,包括机械动量和电磁动量。
显然,右手边因此是单位时间内从该区域流出的总动量,即动量通量。
因此,张量
也被称为动量流密度张量。
在表面上,动量引入了力。
在给定法线方向为
的面积上,回顾力积分项:
在单位面积上,令
为 1:
该矢量被称为应力矢量,代表作用在表面单位面积上的力。
此外,法向分量构成了压强:
7.3 角动量
基于动量,引入角动量:
8. 电磁波 (EMW) 8.1 一维波
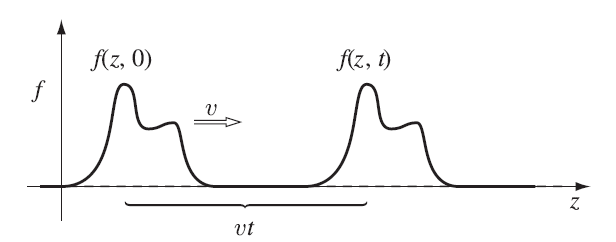
波是连续介质的一种扰动,它以固定的形状和恒定的速度传播。假设介质点偏离平衡位置的位移为
。从图中我们可以得到:
一维波示意图
令
。我们对函数
求导:
二阶导数为:
显然,这些方程产生了标准波动方程:
如果我们指定满足以下条件的两个参数
:
该方程的一个本征解为:
其中
是包含初始相位的复振幅。由于指数函数构成本征态,任何形状的波都可以分解为具有不同
但具有相同速度
的指数波分量:
允许延伸到负区域。在
保持正值的情况下,
意味着
。显然,
的分量对应于向
方向传播的波。
通过固定本征波
中的
,显而易见,当
提供
的相位偏移时,介质点将返回其初始状态。因此,可以推导出周期
:
类似地,固定
。当
提供
的相位偏移时,
处的点表现与
处完全相同。这样的长度被称为波长,用
表示:
这两个基本参数
和
分别被称为波数和角频率。
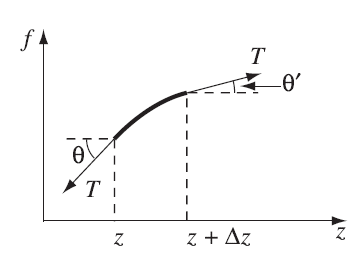
不同的介质承载波的能力不同。假设介质点的回复力是由张力
提供的。
波中的张力
我们有:
此外,假设线质量密度为
。
然后我们得到波动方程:
与标准方程相比,我们得到波速:
我们可以得出结论,介质类型决定了波速。
8.2 偏振
在现实中,三维波更具实际意义。在三维空间中,本征波为:
你只需将各个方向组合在一起,因为它们是相互独立的。
三维波有两种类型。
介质点的位移与传播方向垂直的波称为横波。介质点的位移与传播方向平行的波称为纵波。
对于三维横波,其位移有两个可能的基方向。
如果位移沿
:
沿
:
位移也可以沿
平面内的任何方向振荡。假设矢量为
(且满足
):
8.3 真空中的电磁波
在真空中,没有自由电荷(
)或电流(
)。Maxwell 方程组简化为:
对第二个方程取旋度,
:
使用矢量恒等式
。由于
,我们有:
另一方面,代入第四个 Maxwell 方程
:
使
的两个结果相等,对
进行类似处理,我们得到波动方程:
回想标准三维波动方程
,将其与
和
的方程进行比较,得到波速:
在真空中,该速度被记为光速
:
本征波解为:
由于波动方程是从 Maxwell 方程组推导出来的,所有解必须满足 Maxwell 方程组。应用
和
:
对于沿
方向传播的波,这要求
分量消失:
由于
和
的
分量消失,电磁波是横波。这种最简单的本征波被称为单色平面波。
此外,应用 Faraday 定律
,我们得到振幅之间简洁的关系式:
方向并没有什么特殊之处。通常,单色波为:
其中
沿传播方向。
能量密度
为:
将
和
代入表达式:
复数表达式不能直接测量;模是振幅,辐角是相位。测量得到的是实部。
当波传播时,它随之携带能量。能量流密度由 Poynting 矢量表示:
对于沿
方向的单色波:
动量密度
为:
由于光的电场
(一种电磁波)变化极其迅速,我们关心时间平均值(
),类似于交流电路中的有效值。
平均能量密度:
平均 Poynting 矢量:
平均动量密度:
单位面积的平均功率被称为强度
:
动量产生压强。辐射压
为:
8.4 衍射
解决衍射问题的根本方法是在给定边界条件下求解波函数。考虑
或
的任意分量,记为
。
满足波动方程:
对于频率为
的单色波,
。定义波数
。代入得到 Helmholtz 方程(在波源处,作为边界方程):
这里突然出现撇号(prime)可能会令人困惑。事实上,在没有电荷的任何地方
都满足 Helmholtz 方程。但在衍射问题中,根据 Huygens 原理,我们将孔径上的入射波视为波源。因此,孔径上的波作为边界条件。我们通过 Green 函数法导出整个空间中的波。现在选择一个 Green 函数,即位于源点
的单位源产生的球面波:
其中
。它满足:
应用 Green 第二恒等式:
将
和
替换为:
则:
为了进一步计算,我们需要
。
在光学视角下,
,则
。
假设入射波是来自
的球面波:
类似地:
将所有项代入
:
这个方程被称为 Kirchhoff 方程。
衍射配置图
在远距离处,
,
。被积函数简化为:
8.5 物质中的电磁波
在线性介质中,麦克斯韦方程组(Maxwell equations)变为:
当没有自由电荷和电流时,方程组简化为:
随后的一切推导都与真空中的情况相同。唯一的区别是:
被称为折射率(index of refraction)。在将
、
替换为
、
后,所有结论都一致。
能量密度
为:
坡印廷矢量(Poynting vector)
为:
强度
为:
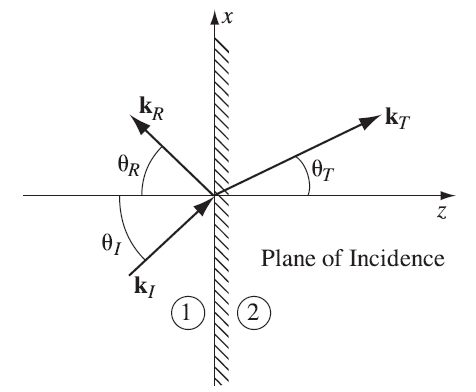
一个有趣的问题是波在边界上的行为。根据边界条件:
现在定义入射波(Incident)、反射波(reflection)和透射波(transmission)。
入射波:
反射波:
透射波:
边界处的行为
在边界处定义
,即仅包含
分量。那么在任意点
,三个场分别为:
应用切向边界条件:
该方程对任意
均成立。因此,指数项必须满足:
入射波和反射波具有相同的速度,因此
。所以:
我们推导出了反射定律。接着,
,
。
所有波共享相同的
。那么对于入射波和透射波:
我们推导出了折射定律,也称为斯涅尔定律(Snell's law)。
处理完指数因子后,它们相互抵消。切向边界条件变为:
通常,
和
被分解为
和
分量。相对于入射面,
偏振定义为
垂直振荡,而
偏振为平行振荡。
对 均 相 同 对 各 不 相 同
对于
偏振,切向电场条件为:
磁场条件为:
代入
和
:
由于
:
总结
偏振的方程组:
对于
偏振,方程组为:
分别求解它们。
反射系数(
)和透射系数(
)为:
回想斯涅尔定律,它在任意
下都成立:
实验发现,在某个特定的
下,
会消失。将该角度记为
。我们有:
斯 涅 尔 定 律
推导如下:
根据斯涅尔定律代入
:
的比值为:
这个角度被称为布儒斯特角(Brewster angle)。在这种情况下:
这意味着在此入射角下,反射波和透射波是垂直的(
)。
入射波会迫使受保护介质中的粒子(视为偶极子)发生振荡。
偏振波引起入射面内的振荡。然而,偶极子不会沿振荡方向释放能量。
在第二种介质中,偶极子由透射波驱动。当
时,反射方向与振荡方向重合。因此,没有能量发出。
这四个系数被称为菲涅耳系数(Fresnel coefficients)。对于任意偏振波,我们定义:
入射电场:
反射电场:
能量反射率
:
透射电场:
能量透射率
:
根据能量守恒:
8.6 吸收(Absorption)
导体通常会吸收电磁波的能量。这里没有束缚电流或电荷。自由电流不为零:
麦克斯韦方程组变为:
此外,根据连续性方程:
解出
:
任何初始电荷都会消散。对于完美导体,
。没有电荷积累。在这种情况下:
波动方程变为:
单色波
和
仍然成立,但波数引入为复数,即
。
通常:
虚部
导致波随空间衰减。特征衰减长度,也称为趋肤深度(skin depth),定义为:
在介质和导体的边界处:
对于非完美导体,过程非常相似。我们假设入射波垂直于表面,因此
。根据切向条件,且
:
入射波:
反射波:
透射波:
假设入射波垂直于表面,因此
。
根据切向条件,且
:
且
:
解出系数:
反射系数
:
透射系数
:
比值
决定了反射/透射特性。
对于完美导体,
,趋肤深度
。
,
。
则
,
。
如果
(非磁性),那么
,
。
这里
是复数。
。
8.7 色散(Dispersion)
有时波的速度取决于其频率。这种现象被称为色散,支撑波的介质被称为色散介质,这是介质的一种自然特性。
在色散介质中,由一定频率范围组成的波会改变其形状。
单一频率代表一个单色波,它以相速度(phase velocity)传播:
波包作为一个整体以群速度(group velocity)传播:
现在我们深入研究色散。我们假设电子被二次势限制在平衡位置。
束缚力为:
显然,实际电势是
,而不是
。我们的目标是描述电子的微小振荡。实际上,任何势能都可以展开:
在平衡点,
。取平衡处的势能作为参考,则
。
因此,对于微小扰动,
。
电子在运动过程中受到阻尼。
阻 尼 是阻尼系数。此外,外部电场
驱动振荡。
驱 动
得到运动方程:
解为:
的振荡产生偶极矩
。假设每个分子拥有
个具有固有频率
的电子(
是介质的第
个固有频率)。
单位体积有
个分子。总极化强度为:
极化率定义为:
因此:
此时介电常数是一个复常数,那么反射率:
也是一个复数。波数:
的实部对
的实部有贡献,作为原始波数起作用,决定波长。
的虚部对吸收有贡献。衰减项为
。
衰减系数
为:
因子 2 是因为
。
利用这些关系推导
与
的关系:
分离实部和虚部:
通常,可见光的
远大于
。吸收非常微弱。在这个区域我们可以忽略
。
由于
,可以展开
。
定义:
则:
将
吸收进
:
这被称为柯西公式(Cauchy's formula)。
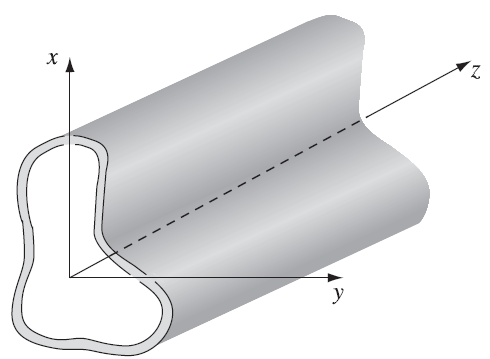
8.8 波导(Guided Waves)
考虑限制在空心管内部的电磁波。这种空心管被称为波导(wave guide)。它是一个完美导体,因此内部
,
。内壁处的边界条件为:
波导
上述两个方程是对空腔内电磁波的约束。电场产生法向条件:
导体中的
为 0。为了满足条件,在内壁上会感应出自由电荷和电流。假设电磁波:
它们满足:
按分量求解:
当我们对
进行
操作时,得到:
对于
同理:
因此,我们可以用
和
替换
和
算符来简化。
波动方程得到:
在波导中,
和
不能同时为零。
如果
:
如果
:
对它们求二阶导:
只有当
常 数 ,
常 数 时它们才同时成立。然而它们是振荡的。
证毕(Q.E.D.)。
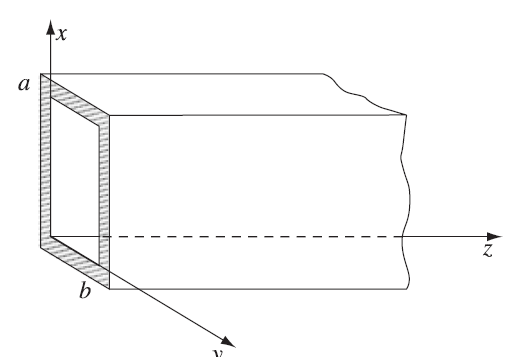
我们以矩形波导为例。令
且
。
矩形波导
所以:
除以
:
其中:
由于
,解为:
要求:
代入得:
结果为:
同理可得
:
则:
注意
的空间频率是离散的,这是周期性边界条件的必然结果。(
) 构成了波导中电磁波的模式(modes)。
在模式
下:
如果满足以下条件,波数将变为虚数:
被称为该模式的截止频率(cut-off frequency)。任何频率低于
的分量都会被波导吸收。最低频率
或
被称为主模(dominant mode,取决于哪个更小)。
在上述推导中,我们设
,这意味着
是横向的。此类模式记为
。如果我们设
,推导完全相同,会得到一组完全不同的模式,记为
。
当频率为
的单色波进入波导时,能量会立即重新分配到
所 有 模式,包括
和
。只有满足
的模式才能通过,而其他模式会被吸收。
在波导中,能量传播由坡印廷矢量决定:
我们只关心沿
轴的传播。我们将
分解:
其中
在
平面内。提取
的大小:
和
构成一个希尔伯特空间。检查不同模式下
的内积:
这可以证明不同模式是否相互影响。
现在来证明这一点。在
模式下:
平面内的场:
取两个模式的内积:
同理:
也有相同的结论。那么:
我们可以说不同模式是正交的。
回到单色波。由于正交性,电场(EF)应该按模式分解:
系数由下式决定:
我们没有考虑入射角,因为模式本身就是反射、折射等作用的结果。角度信息已经编码在
之中。
9. 辐射 9.1 规范不变性
由 Maxwell 方程组,
它可以写成无旋的形式,
利用
和
,可以导出
结合
场
可以直接从势
导出。但对于特定的
,
并不是唯一的。假设两组势
和
,
我们假设它们给出相同的
,那么
我们可以将
写成某个标量的梯度,
则
括号中的项因此与位置无关,
其中
仅取决于时间。我们可以将
吸收进
中,而不会产生其他影响。
那么
因此,任何标量函数
都可以改变
并得到另一组给出相同场
的势。这种变换被称为 规范变换 (Gauge transformation)。
有两种常用的规范,分别称为 Coulomb 规范和 Lorentz 规范。
在 Coulomb 规范中,我们选取
由此,
在 Coulomb 规范中,标量势由当前的电荷分布决定,这似乎与相对论的传播速度限制
相冲突。为了解释这一点,需注意
不是一个可测量量,可测量量是
。然而
当
变化时,
也会变化,从而抵消了
的部分变化。最终,
以速度
传播。在 Coulomb 规范下,
易于计算但
较难。在 Coulomb 规范中,
的微分方程为
在 Lorentz 规范中,我们选取
这是为了简化
和
的方程而设计的。由此,
同时
变为
我们可以注意到
和
遵循相同的形式。
这些方程被称为 d'Alembert 方程。
Lorentz 力可以用势来表示。
的导数项
被称为
的对流导数,记作
。
那么
电动势为动量和能量引入了一些额外项。我们定义正则动量
和依赖于速度的能量
9.2 推迟势
电磁效应以速度
传播。因此,如果观察者在场点
观察到电磁效应,它是早些时候在源点
产生的。延迟时间为
那么在时间
,我们在
处观察到的效应发生在
该时间被称为推迟时间。电势的一个自然推广是
这些被称为推迟势。它们满足 d'Alembert 方程吗?
且
其中
取散度
因此
标量势满足 d'Alembert 方程。
同理。因此,推迟势是 Lorentz 规范下的有效电势。
给定推迟势
显而易见
并且我们已经计算了
的梯度。利用
至于
,我们先求
那么
这两个方程被称为 Jefimenko 方程。
当电荷加速时,它们的场会将能量传输到无穷远处,这被称为辐射。假设源位于原点附近。通过闭合表面的功率为
电磁波以速度
传播。能量在
时离开源。那么,
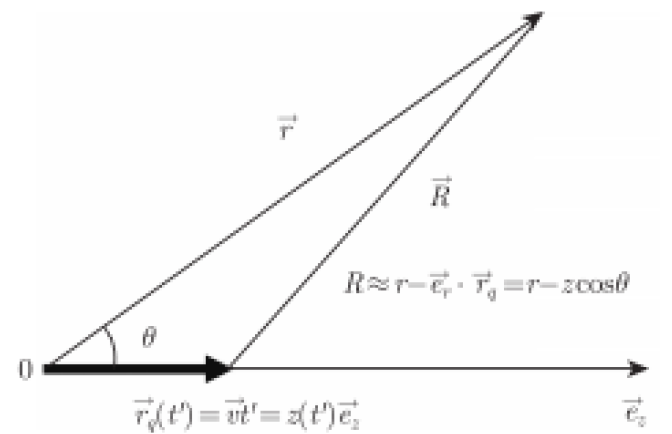
9.3 特定辐射场
交流电带来周期性的电流和电荷
代入推迟势
其中
根据辐射的定义,我们应当使
。然后进行近似。
代入近似值。
进一步展开
我们从 Lorentz 规范推导
和
。
考虑
的第
项
则
那么
可以按阶分解。
一个周期内的平均 Poynting 矢量(类似于交流电中的有效值)
辐射功率
显然,对于
,被积函数变为 0。因此,只有
项对辐射有贡献。那么电势可以简化为:
磁场
我们忽略了
中的高阶项。类似地,我们得到标量势。
根据
以及
则
平均能量流密度
以及辐射功率
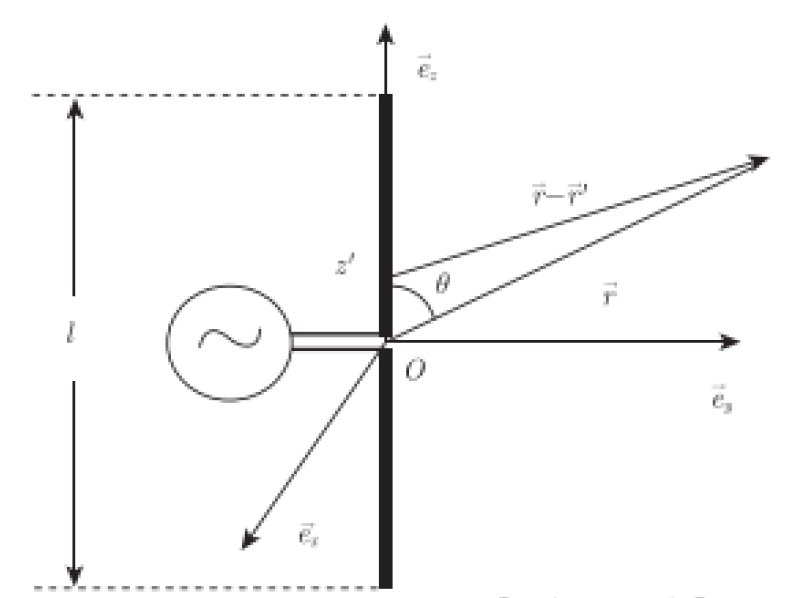
假设天线的长度为
。取中点为原点。变化的电流从原点输入。天线是良好的导体。
细直天线
天线内部的电场为 0。在表面上,
因此
对时间求导,
由于
只有
分量,那么
利用 Lorentz 规范,
我们得到
这是一个波动方程。根据
和
之间的关系,我们可以说
在
处,
。因此
是一个驻波。
其中
。然后我们计算辐射功率。
其中
。当天线很小(
)时,我们用
进行近似。
总功率为
辐射功率随
的增加而迅速增加。
的天线被称为半波天线,此时
。代入得,
辐射最强的方向可以通过下式确定
我们得到
是最强的。
假设系统尺寸
,其中
是电磁波的波长。同时
。在此条件下,我们利用
展开
。
第一项对应偶极辐射,第二项对应四极辐射。
我们先检查偶极子。我们计算
两边积分。
被积函数等于零,因为在表面上
。因此,
故
磁矢势
场
Poynting 矢量
那么
接下来我们处理四极子。考虑
的第二项
我们重点关注这两项。首先考察:
那么
则
且
对时间求导,
负项
那么二阶势,
被分离为四极子贡献和磁偶极子贡献。对于四极子,
对于磁偶极子,
10. 电动力学中的相对论 10.1 狭义理论 Maxwell 方程组预言光在某种介质中传播。人们曾认为这种介质是以太,一个绝对静止的惯性参考系。但 Michelson-Morley 实验否定了以太的存在。为了解决这一冲突,Einstein 提出了两个著名的公设。
相对性原理:物理定律在所有惯性参考系中具有相同的形式。
通用光速:真空中的光速对于所有惯性观察者都是相同的
第一条陈述指出不存在绝对静止系统。第二条指出不存在以太。
现在基于这两个公设,我们推导相对论中的坐标变换规则,称为 Lorentz 变换。经典力学中的变换称为 Galileo 变换。
取两个惯性参考系
和
。
沿
轴正方向以速度
运动。假设
,
,
,当原点
和
重合时,
。
假设变换是线性的。那么对于任何事件
由于在
和
方向没有相对运动,
光信号在
和
处出发。在两个方向、两个参考系中,通用光速分别给出:
正 向 负 向
同时,
的原点在
中以速度
运动。
在
中的坐标为
综合所有方程,我们以矩阵形式改写它们。
由于
,
且
同理,负向光给出:
联立两者
我们还有
。那么
给出
我们可以将变换重写为矩阵形式
该变换不应缩放或反转方向,因此,
现在我们可以求解系数。为了简化,我们定义两个因子。
结果为:
Lorentz 变换因此为
逆变换应保持形式。将
替换为
并交换坐标
然后我们可以推导速度变换
逆变换为
我们考虑
也是一个维度,因此空间变为四维。我们记
中的坐标
在
中为
Lorentz 变换读作
使用张量符号,我们可以记作
其中
称为 Lorentz 变换矩阵。
如果速度的方向改变,Lorentz 变换矩阵转变为三维版本
其中
。
现在我们定义四维矢量的内积。假设光在真空中传播。在
内,它行进的空间距离为
由于光速在所有惯性参考系中保持恒定
,那么
我们重写为
对于特定事件,该方程在所有惯性参考系中都成立。很自然地,我们定义两个事件之间的时空间隔
由于它是 Lorentz 变换的根源,该假设是成功的。那么四维矢量的模定义为
内积也是自然的
该定义是良好的,因为它在 Lorentz 变换下保持不变
模是内积的一个特例。这意味着时空间隔在 Lorentz 变换下保持不变。
我们一直使用逆变矢量。引入协变矢量 Tensor Algebra 。
这样的定义保持了内积
引入度规
根据定义,度规张量因此为
称为 Minkowski 度规。该时空空间称为 Minkowski 空间。Minkowski 空间是一个伪欧几里得空间。利用度规张量,
由于 Minkowski 空间不完全是欧几里得空间,内积不是正定的。它可以是正的(空间项占主导)或负的(时间项占主导)。我们定义两个事件的位移
其模可以是正或负。我们进一步定义
如 果 称 为 类 空 的 如 果 称 为 类 时 的 如 果 称 为 类 光 的
其中
是事件 A 和 B 的时空间隔。回顾光速不变原理,它还告诉我们信号传播速度不能超过
。现在,如果事件 B 是由 A 引起的,那么它们必须能够被亚光速信号连接。数学上
这意味着
即,
因此,类时事件意味着 A 和 B 之间的因果关系在物理上是允许的(但不一定)。同样,如果间隔是类空的,因果关系是不允许的,事件的顺序在 Lorentz 变换后可能会改变。类光事件在建立因果关系时必须以光速连接。信号必须具有零质量。类光是因果关系的限制。
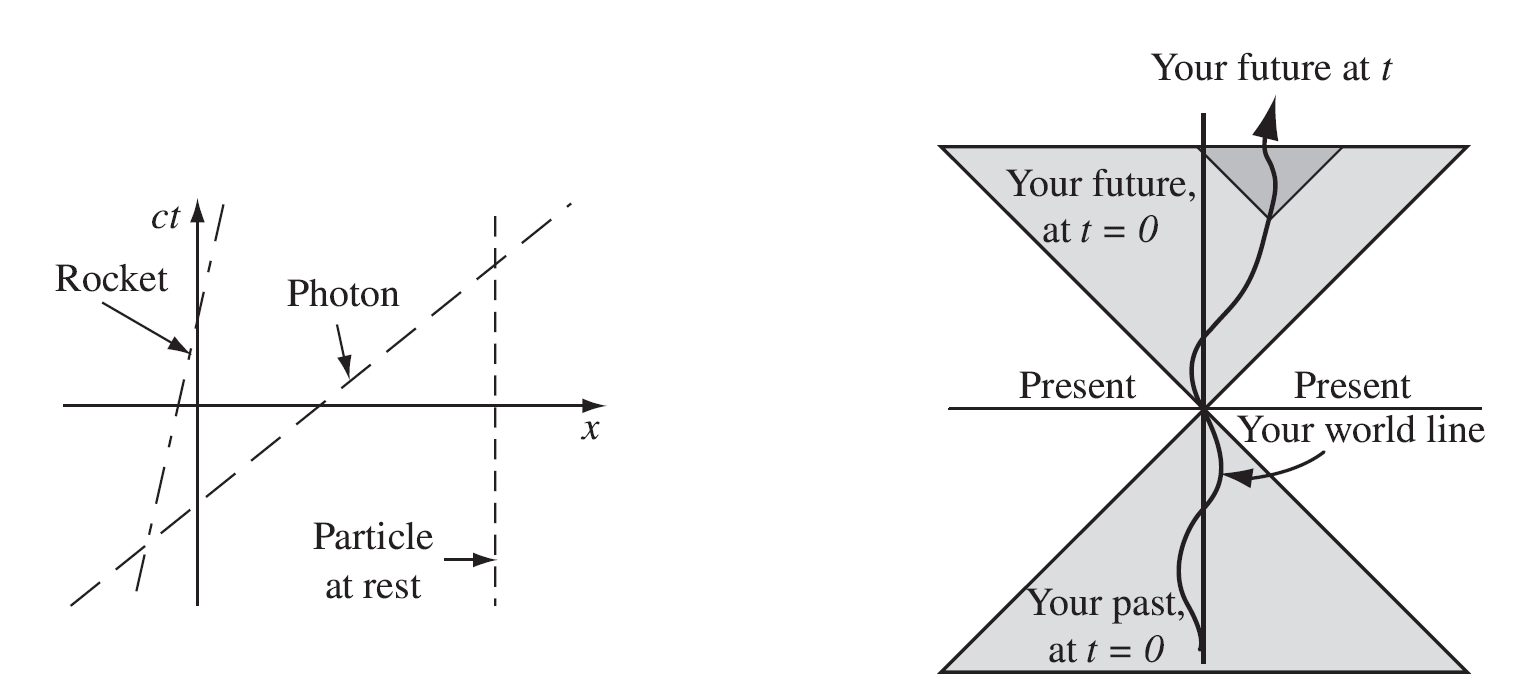
我们可以通过 Minkowski 图图形化地表示运动。我们将空间坐标水平绘制,时间坐标 (
世界线与光锥
Minkowski 图上的轨迹称为世界线。如果粒子处于静止状态,其空间坐标随时间流动保持不变。那么它的世界线是垂直的。类光事件发生在
上,这是一条斜率为 1 的直线。由于没有粒子旅行速度能超过
,因此斜率小于 1 的世界线是不允许的。假设你从
的原点出发。两条类光线
(正向运动)和
(负向运动)定义了物理允许的你的过去和未来。
你 的 过 去 你 的 未 来 你 的 现 在
该结构在几何上形成一个锥体,称为光锥。如果包含
和
,它将是一个超锥体。
在 Minkowski 图中,我们选择两个事件并计算它们的时空间隔。其中一个事件作为参考。在超锥体中,我们假设在
时两个事件发生在同一位置(时空间隔
)。但在大多数情况下并非如此。在
时,它们通常有一个初始时空间隔。
当
时,意味着位移是类空的。在
时,它们发生在不同的位置,不允许因果关系。由于
,它们分别发生在
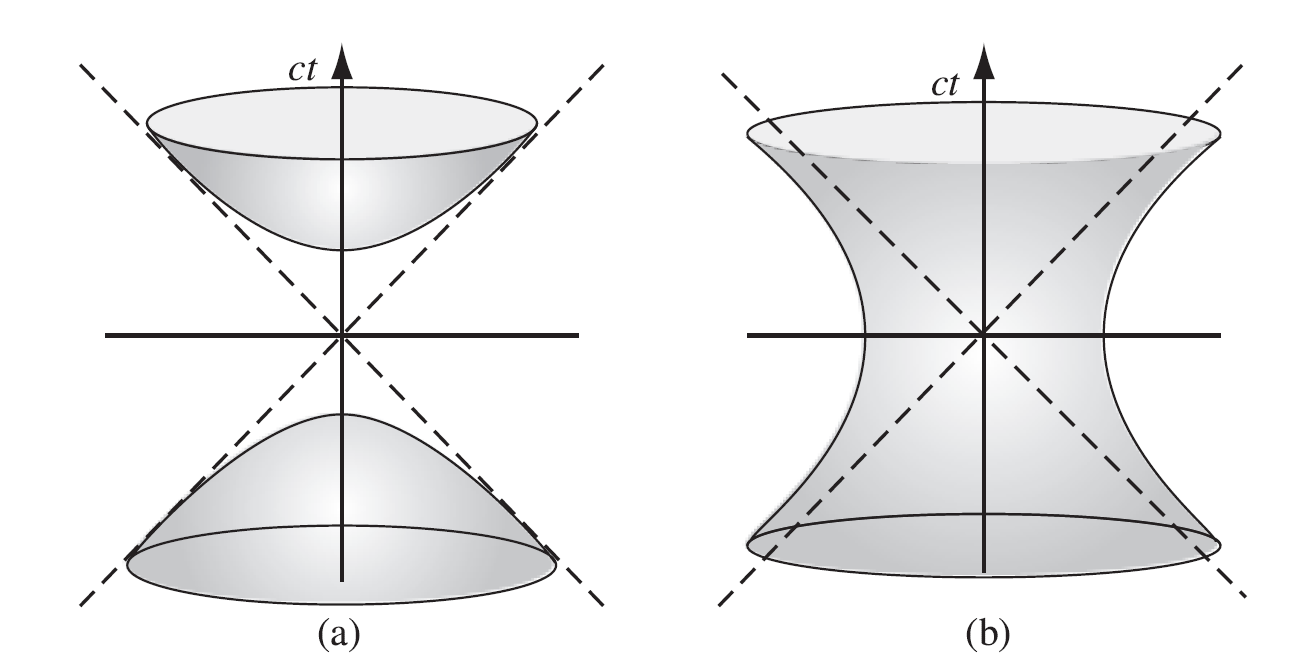
。光锥向外倾斜,变成以空间子空间为焦点的双曲线(在 4D 空间中为双曲面)。
当
时,是类时的。在
处,它们发生在不同的时间
。Minkowski 图也是双曲线 / 双曲面,但焦点在时间轴上。
Minkowski 图中的双曲线和双曲面
在 Minkowski 空间中,Lorentz 变换是一种伪旋转。利用度规,
这等价于
矩阵形式为
记逆矩阵为
,满足
由于
是伪正交的,
。那么
那么,对于逆变矢量
对于协变矢量
重新分配索引,我们有
现在我们考察 Lorentz 变换下的张量。我们从收缩得到的标量开始
在 Lorentz 变换下,
应保持不变
矢量被变换:
代入
消去
和
:
那么
但如果
是全逆变的,条件变为:
代入
那么
进一步
10.2 相对论力学
在 Minkowski 空间中,四维速度定义为
其中
称为原时,代表粒子感受到的时间(在与粒子一起运动的参考系中的时间),这是特定粒子的固定参数。同时,这意味着
在 Lorentz 变换下是常数。那么四维速度定义为
应用 Lorentz 变换矩阵
现在有一个有趣的结论。对于任何粒子,四维速度的模是常数。
它表明在 4D Minkowski 空间中,所有粒子都以速度
沿其世界线“流动”。如果空间速度不为
,速度在时间轴上的投影将变小,原时变慢。
现在放置一个惯性的静止观察者,其速度为
Minkowski 空间具有标准正交基。
时 间 空 间 正 交
当然我们还有其他空间基矢量,但一个就足够我们的推导了。假设观察者参考系中的 3D 空间速度为
定义时间膨胀因子
在 Minkowski 空间中,由于时间膨胀,速度在空间子空间上的投影不是
那么
结合
应用模条件
最后
那么我们知道
这就是时间膨胀。原时比参考系中的时间(我们称之为“普通”时间)慢。请注意
因子中的下标
,不要将其与以速度
运动的坐标系引入的因子混淆。在接下来的章节中,我们将称运动参考系 (
) 中的参数为“固有”参数,称参考系 (
) 中的参数为“普通”参数。
除了时间膨胀,在
系(Minkowski 空间中的参考事件)看来,运动的尺也会变短。考虑一个长度固定为
的杠杆。我们想同时测量两侧的坐标,因此,测量必须由两个事件完成。在静止参考系
中,杠杆两侧的世界线分别是
和
。动态参考系
沿
以速度
运动。我们将在
中测量杠杆并得到测量长度
。
在
中,我们要求两个测量事件满足
。假设在
中,左侧事件是
,右侧事件是
。Lorentz 变换给出
在
中,
,
因此
因此在
中,这两个事件的时间差是
。在
中,4D 位移是
通过 Lorentz 变换,在
中
第二个分量就是所需的长度
因此在
中,测得的长度比其固定长度短。
为了在所有惯性系中保持动量守恒,相对论动量用固有速度定义。
时间分量自然是
在量子力学中我们已知时间平移不变性对应能量守恒,空间平移不变性对应动量守恒。
(详情请点击链接 Symmetries and Conservations )。
在相对论中,时空平移作用于一个矢量,守恒流也是一个 4D 矢量 ——
。其时间分量对应时间平移不变性,即能量。空间分量则自然是动量。但
不具有能量量纲。所以能量定义为
当粒子静止时,
在运动中,额外的能量是动能。
就像速度一样,在 Minkowski 空间中能量和动量总是守恒的。
用
替换
,那么
Minkowski 空间中的力是
空间力
是我们实验中测量的机械力,其中
是相对论动量。第一项
代表传递给粒子的功率。
在相对论中,经典力学中的质心被质能中心取代。
总动量为
10.3 相对论电动力学
Maxwell 方程组在 Lorentz 变换下已满足相对论。为了证明,我们需要将 Maxwell 方程改写为张量形式。配置一个参考系
,另一个参考系
以速度
沿
的
轴正方向运动。我们有 Lorentz 变换
根据链式法则,我们有
在
中,
将导数变换到
中
电荷守恒在所有惯性系中都成立。假设变换是线性的。
在
中
代入并比较相应系数,
表明
满足 Lorentz 变换。如果我们构造四维电流密度
它满足
电荷守恒变为
是
的四维散度。所以它指出电流密度在四维空间中是无散的。
有了
,我们就可以定义四维势
我们现在需要一个场的张量(2 个场)。我们知道在经典理论中
和
是由
和
的导数组合而成的。在 4D 空间中,自然使用四维导数。
需要规范不变性。场张量在规范变换
下应保持不变。然而,
不是规范不变的。但反对称量
是规范不变的,因为
。通过这个定义,分量很容易求得。
对于
对于
,空间分量
展开形式为
为了简单地表达物理定律,我们构造
的对偶张量。用
替换
,用
替换
。
利用这个张量,Maxwell 方程可以改写为
这两个简单的方程实际上包含了所有 4 个 Maxwell 方程。为了验证,我们展开它们。
第一个方程
它们分离为
第二个张量方程展开为:
它们分离为剩下的两个 Maxwell 方程:
所以张量方程等价于 Maxwell 方程。在 Lorentz 变换下,张量遵循变换规则:
根据
,Minkowski 力是
对于
,
因此,实验力是
这就是 Lorentz 力。
回想在 Lorentz 规范中,
以及四维势
计算 Minkowski 空间中的散度:
那么
这给出:
匹配 d'Alembert 方程。我们可以看到 d'Alembert 算子
实际上是 Minkowski 空间中的 Laplace 算子。
10.4 Doppler效应
当波源运动时,波的频率可能会改变。我们采用相同的参考系配置:观察者在
中,波源在
中,以速度
沿
运动。在
中,固定频率为
且
。其相位是一个 Lorentz 标量
其中
是四维波矢量
它必须遵循 Lorentz 变换
假设
,因此
应用 Lorentz 变换
获得频率变换
在参考系
中,
代入频率
观察者看向波源。由于光传播方向与视线相反,那么视线与
的夹角
为
那么观察到的频率为
这被称为Doppler效应。
11. 带电粒子与 EMF 的相互作用 11.1 Liénard-Wiechert 势
通常电磁系统的标量势
和矢量势
由推迟势给出。现给定一个以速度
运动的点电荷。其电荷密度和电流密度为
在
处观察,标量势仅取决于点电荷在
的状态。因此
。标量势为
这里有一个技巧:当
时,
。然而,
也是
的函数。那么当满足以下条件时
等于 1:
为了求解这个复合函数,我们引入一个
。
函数在以下情况等于 1:
空间条件:在
时间条件:从
即,
函数可以被分解
注意到出现了一个雅可比行列式系数。先计算它
其中
那么标量势
矢量势
同理
这些标量势和矢量势被称为 Liénard-Wiechert 势。如果我们用相对论符号表示
则
基于 Liénard-Wiechert 势,可以得到电场强度
和磁感应强度
。我们令
并先做一些准备工作。
在推迟势中,推迟时刻
。那么
现在计算
和
11.2 带电粒子的辐射
在第 9 章中我们已经知道,在
和
中只有
项对辐射有贡献。那么忽略所有高阶项。
显而易见,如果
则没有辐射。通常情况下,Poynting 矢量:
在
时间内,在
处发射到
的能量为:
通常情况下,观测时间
并不是那么方便。最好使用推迟时刻
,即能量实际发射的时间。在
时间内
总功率
被称为 Liénard 公式。
回顾 Poynting 矢量
通常它包含许多频率分量。我们通过 Fourier 变换将它们分离。
对辐射有贡献的场是
频谱
发射功率为
总发射能量
那么在单位立体角内,能量谱为
辐射引起机械能的衰减。辐射功率由下式给出
能量守恒要求
的效应可以等效为一个阻尼力。
忽略相对论效应:
代入
取时间平均是因为
是一个等效力,并非在任何时间都精确正确。取一个伪周期
。
比较两边,
这个力被称为 Abraham-Lorentz 辐射阻尼力。这个力是一个等效量。既不是在所有系统中,也不是在任何时间
。
回顾辐射功率
考虑一个在真空中运动的带电粒子。既然没有力作用在它身上,运动应该是匀速的。
将此代入辐射功率,我们发现
因此,真空中的粒子不辐射。
11.3 谱线展宽
原子发射能量,大多数情况下是以光子的形式。在实验中,单色光的波谱自然地变宽,这令许多人感到困惑。
我们首先将光子的发射简化为电子的一维谐振。取振荡方向为
轴,
为固定频率
光子的发射可以等效为辐射阻尼力作用在电子上。于是运动方程变为
令
(为了电子不坍缩进原子核)。
我们定义
系数表明
,
。令
。
仅保留
的一阶项。
则
代入得
辐射场
定义
。分解为频率分量。
波谱密度。
峰值位于
。半高宽出现在
则
11.4 散射
在介质中,入射单色平面波应用于原子外层电子的力为
外层电子运动缓慢,因此
(非相对论)。在单色波中:
因此我们可以忽略
的影响。
单色波的电场
运动方程
电子仍然以固定频率振荡。
,代入得
其中
振荡的电子与其原子实(原子核和其他电子,带电
)形成一个振荡的电偶极子。设
为原子实的位置(以电子平衡位置为原点)。
我们之前计算过电偶极子的辐射(在 9.3 节)
其中我们令
,因为原子实的质量远大于
。此外,入射波的强度为
与
的比值被称为散射截面。
存在 3 种特殊情况:
11.5 粒子辐射
轫致辐射是在粒子与材料靶中的原子碰撞并突然减速时产生的。动能以辐射的形式发射。考虑非相对论情况
。
当
时:
减速过程极其迅速。因此
被视为常数。总辐射能量:
那么波谱为
对立体角积分:
同样由于减速非常迅速,
。在 Fourier 变换下:
因此
然而,我们一直在对
进行积分,其中负频率在物理上无法观测,应该折叠到正频段。
这一结果表明轫致辐射的波谱是一个常数。但这仅在
时成立。当
时,
由于
的快速变化而剧烈震荡。正的
和负的相互抵消,导致在
处快速衰减。
这种辐射是由带电粒子在介质中以超过介质中光速的速度运动引起的。假设折射率为
,粒子速度
。电荷密度
,电流密度
。推迟势
展开波谱
取
,
轴满足
。我们关注远场辐射,
。那么
在分母中仅保留
Cherenkov 辐射配置
显然仅当
时,
。因此辐射仅以
发射。辐射场因此是一个圆锥面。
Poynting 矢量
总辐射能量
代入得到空间波谱
引入
是粒子的路径长度,用于解决 delta 函数的平方。实际上
总是有限的。人们关心单位长度的辐射能量。
这个公式被称为 Frank-Tamm 公式。发射的光子数为
过渡辐射产生于带电粒子穿过两个各向同性介质之间的边界时。考虑最简单的情况:真空中带电粒子
向接地的无限大导体平面运动,速度垂直于平面。电势可以用镜像法求解:
假设在
时,
。则:
在
时,粒子到达平面。就在
之后,粒子立即被屏蔽(消失,减速)。在
空间,粒子及其镜像的轫致辐射叠加。
过渡辐射系统的电流密度由粒子及其镜像电荷的叠加给出:
用 Fourier 变换分解:
在远场近似下,推迟势为:
应用
的 Fourier 变换。
代表观测方向。
假设
:
因此波谱为:
对
积分
参考文献: [1] D. J. Griffith, Introduction to Electrodynamics , 4th ed. Cambridge: Cambridge University Press, 2017.Classical Electrodynamics , 3rd ed. New York: Wiley, 1999.