模集集成电路设计

Copyright Notice:

This article is licensed under CC BY-NC-SA 4.0.

Licensing Info:

Title: Analog Integrated Circuits

Author: EleCannonic

Link: https://elecannonic.github.io/categories/electronics/analog_integrate/

Commercial use of this content is strictly prohibited. For more details on licensing policy, please visit the About page.

1. MOSFET

1.1 MOSFET in CMOS

A typical fabrication of NMOS is shown in the figure below.

Sketch of NMOS Fabrication

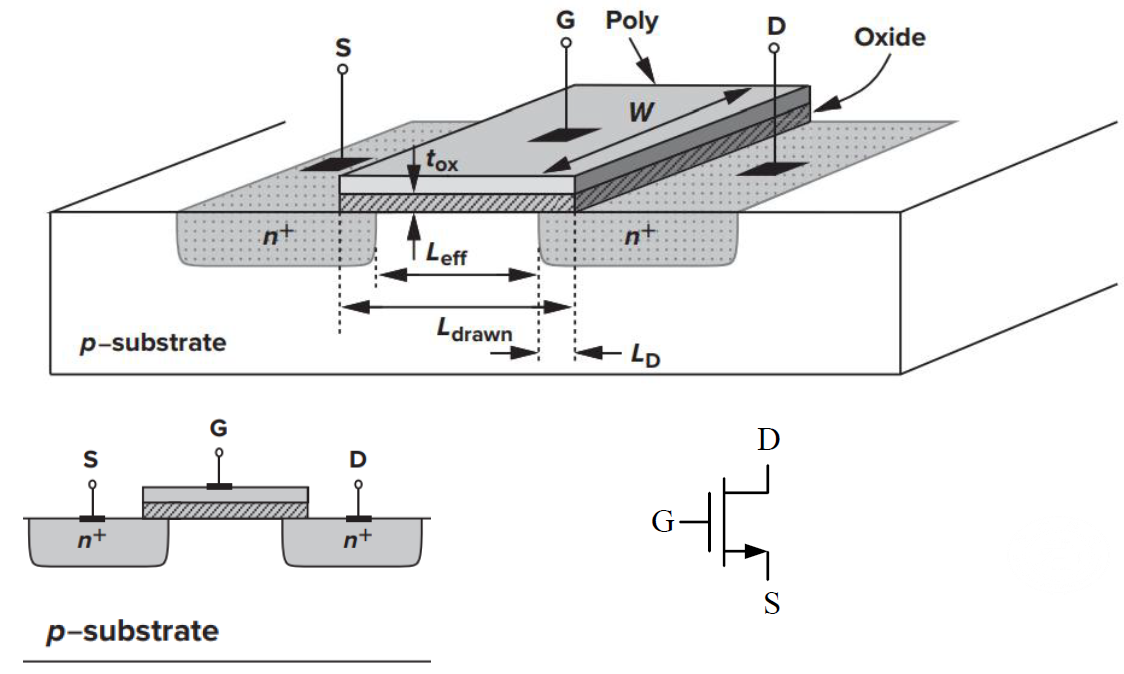
The NMOS is grown on a p-substrate,
which contains as majority carrier.

First discuss cases of

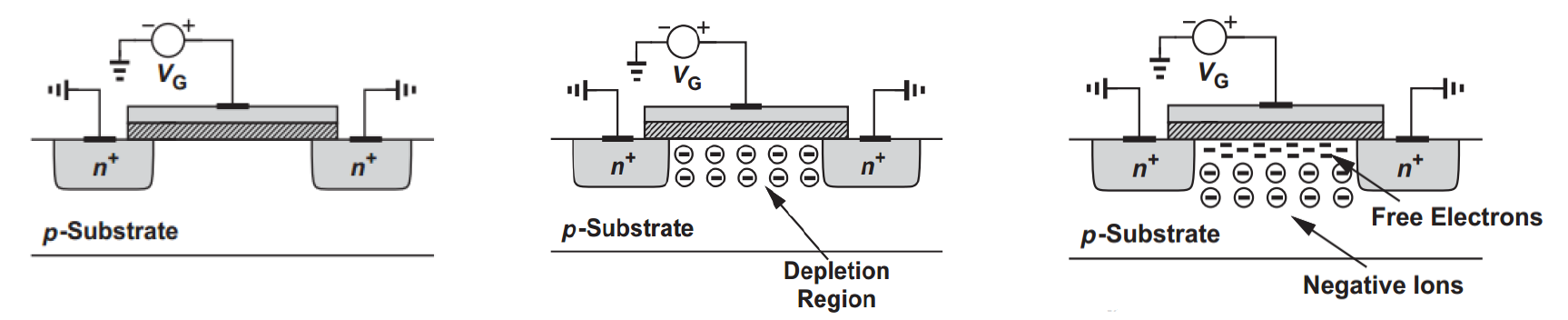
Obviously nothing happens in the NMOS, no electric field. NMOS is cut-off and at equilibrium.

Positive voltage at gate produces a vertical

from

to p-sub.

Some of the minority are attracted to the surface while

are pushed away.

The attracted gather near the surface of p-sub.
However, the is still weak.
It’s not enough to attract adequate to deplete all ,
hence there’s still no free . The MOSFET is cut-off.

Now is strong enough to attract adequate to generate a channel for free .
The MOSFET is on.
On the surface of p-sub,
the ‘s are fully depleted,
the remaining become free ,
forming a conductive channel.

The threshold voltage of to turn on the channel is denoted .

Three Working Region of NMOS

The threshold voltage is related with doping, material and process. Generally,

and

are determined by material and doping concentration of substrate, respectively.

is the charge of depletion zone.

, gate oxide capacitance, is determined by thickness of oxide and material.

PMOS has one more step than NMOS in fabrication. There’s an n-well on the p-sub, then 2 p-semiconductor S and D.

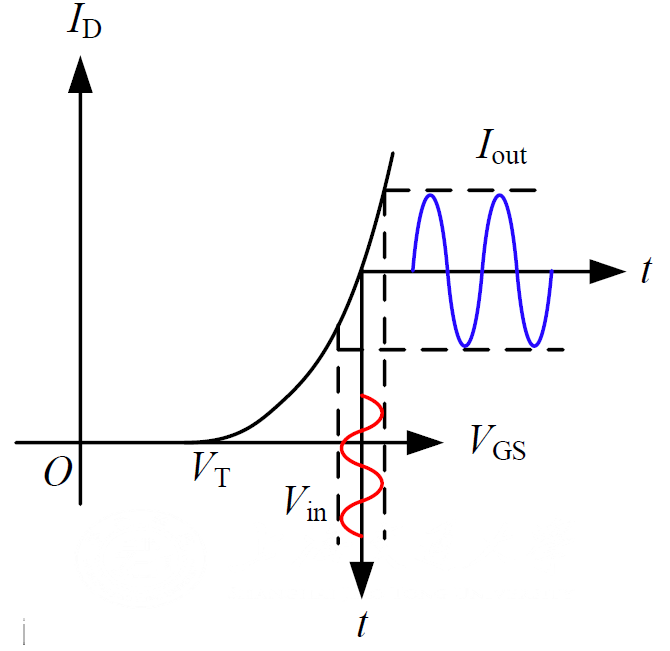
1.2. Large Signal Behavior.

Cut-off: .
.
Weak Inversion / Sub-threshold Region. , but .

With depletion region, there’s no drift current, only diffusion current.

Diffusion current depends on the concentration density of .

The gradient satisfies

It can be deduced.

where depends on the process. is called thermal voltage.

At room temp. .

Triode Region. , .

We can define overdrive voltage

as how much exceeds .

We apply a voltage at D, generating a gradient.

Triode Region of NMOS

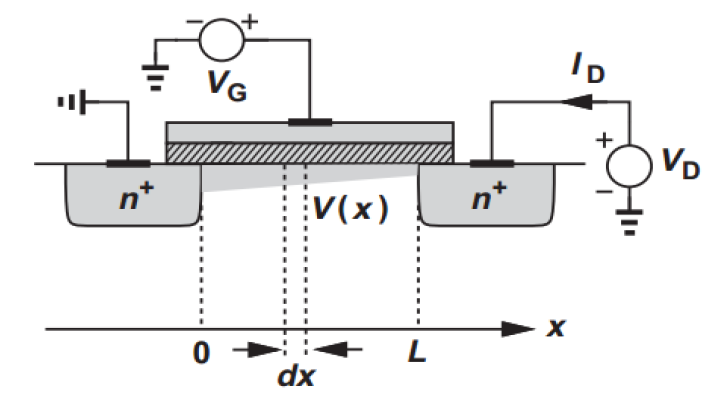
The charge at cross section is (to simplify, regard )

where is capacitance of oxide of unit area. Current is charge over time

Integrate over entire channel length

Hence

Saturation Region

If is very large, while , maybe , causing the pinch-off of the channel between and . The effective channel length may be shortened. In this case, the integral over channel length no longer has upper bound if . Let . we get

1.3 Channel Length Modulation.

Considering pinch-off in saturation region.

is an empirical parameter equivalent to modifying

. We assume

approximately:

In fact

where

only depends on the process, called Early voltage.

Since pinched-off channel is shorter relative to lower device, hence the longer the channel, the weaker channel length modulation is.

1.4 Small Signal Analysis

With a specific DC bias (large signal),
the small signal analysis evaluates how much effect a small variation based on DC bias causes.

Large Signal and Small Signal

The MOSFET small signal equivalent circuit is shown below.

Small Signal Model of MOSFET

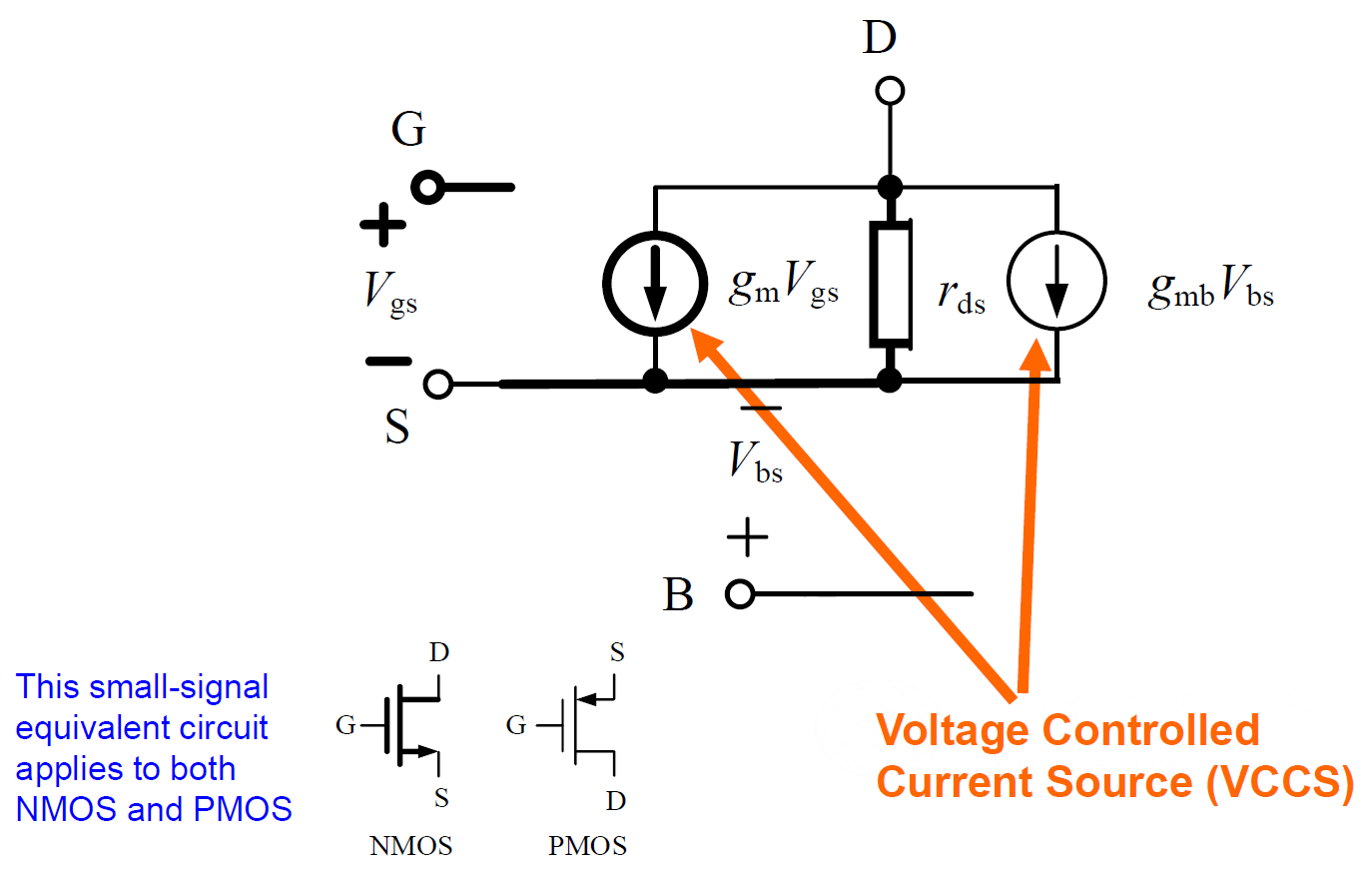
Under DC bias , , and , take a full differential

Approximate (small signal) with .

the three terms represents three current branches. Hence there must be three branches between and . The parameters are determined by the derivatives,

Plug these parameters in

In saturation

Note that . It looks like a conflict that whether is positively or negatively related to . But note that is a constant while is not. So the correct answer is

Since bulk/substrate is always connected to the GND (NMOS) or VDD (PMOS),
to simplify problems, we regard ,
so will cause no effect.
But when the drain (NMOS) or source (PMOS) is not connected to GND or VDD,
this term must be taken into consideration.

Also, the impedances

We hope to have large and large . But they conflict each other when

So we have to balance the two parameters. Define intrinsic gain

Also

From the deduction above, we can have another understanding of the small signal model.

turns the input voltage

into the current

, and then

turns

back to voltage. In fact almost all amplification circuits can be decomposed into the two steps. So the total voltage gain is

We know the small signal voltages are approximation of differential, hence in small signal model, we only take variation into consideration. All constant voltages (DC flatten) in large signal model are considered as AC-GND,
including GND, VDD, bias, and so on.

1.5 Complete MOSFET Small Signal Model

With high freq. input, the capacitance between different parts can no longer be ignored.

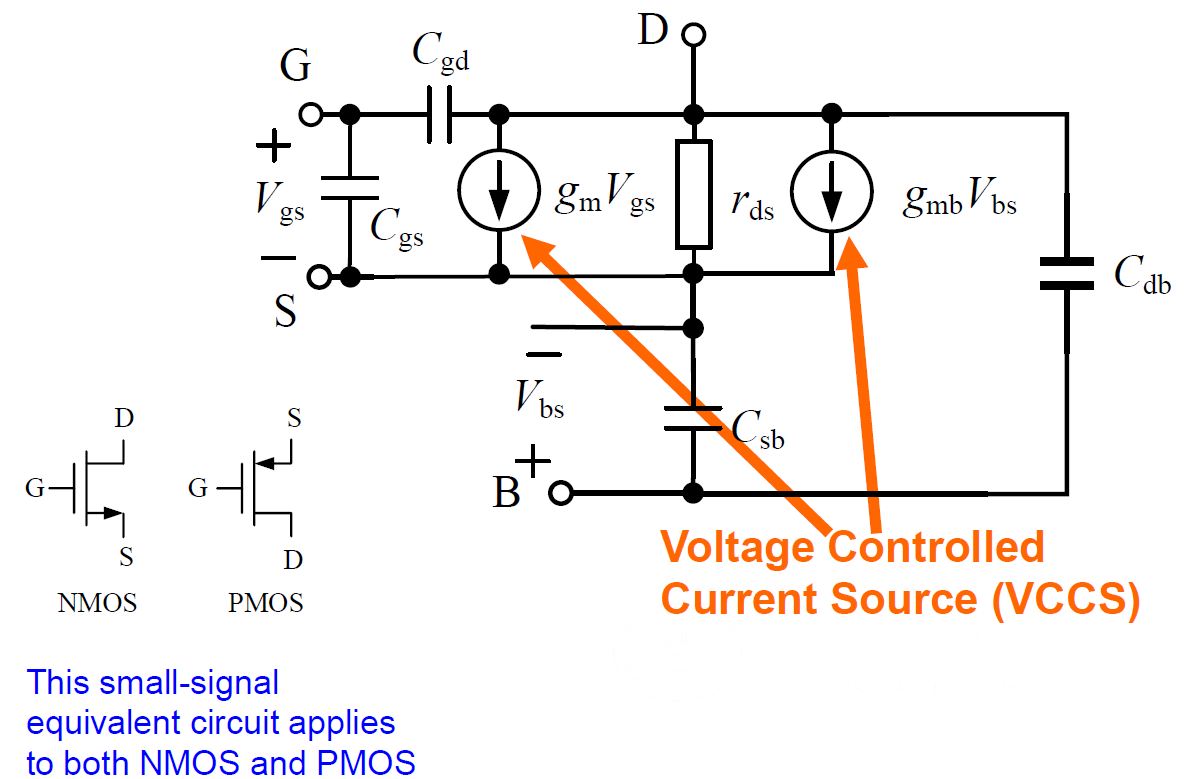
Complete Small Signal Model of MOSFET

2. Single-Stage Amplifiers

2.1 Insight of Amplification

Recall the intrinsic gain of MOSFET small signal model. For more amplification circuit, it can be expanded

So why MOSFET can amplify? For MOSFET.

and

are always large enough. And the model tells us the two parameters are independently controlled by

and

. Meanwhile, recall the curve

DC Resistance and AC Resistance

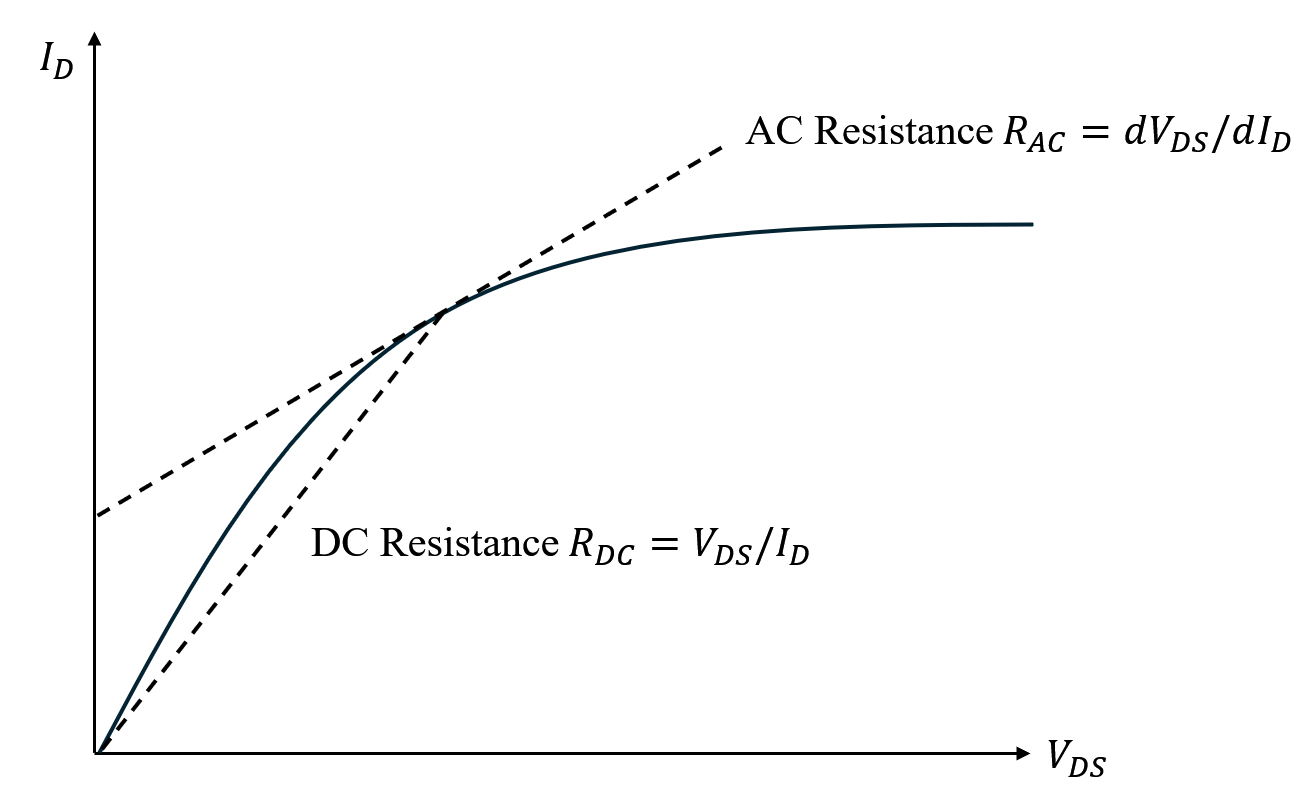
The resistance of large and small signals are separated. The large signal resistance must be finite, while small signal resistance may be infinite (in saturation, approximately). So the separation of DC and AC resistance is also an important reason to amplify.

An opposite example is resistors. Also follow the two steps, voltage to current, current to voltage. For resistors

They’re not independent, and . Finally, the gain is

No amplification.

2.2 Amplifier Concepts

The voltage gain:

The current gain:

The power gain:

There are 4 types of amplifiers.

4 Types of Amplifiers

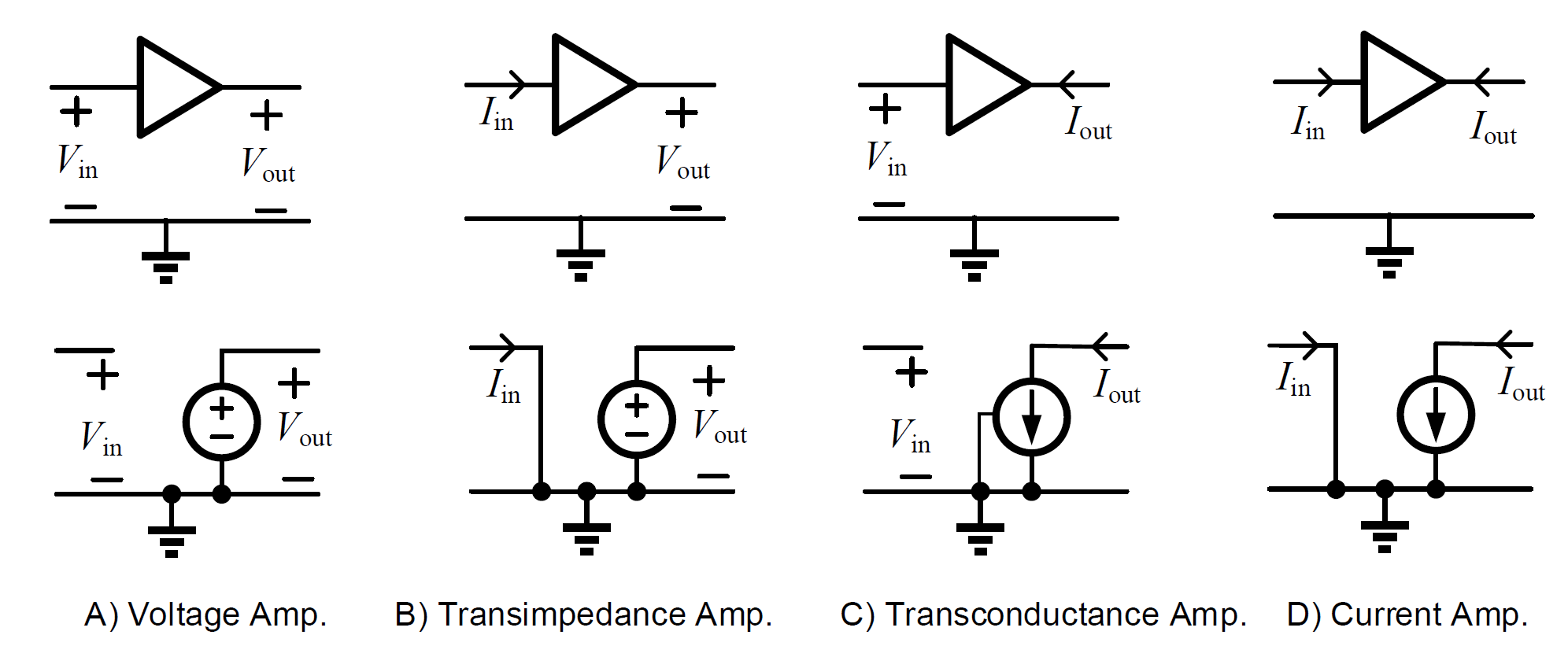
2.3 Three configurations of MOSFET Single-Stage Amplifier.

There are 3 configurations:

Common Source: input G, output D
Common Gate: input S, output D
Common Drain: input G, output S

Note that for all configurations the MOSFET should always be in saturation region.

A MOSFET is a 4-port device. Ignore the bulk, we can list the impedance of the remaining 3 ports (relative to AC-GND)

Gate: , , control current source.
Source: (low impedance), , control current source.
Drain: (high impedance), , can’t control current source.

Originally there should be 6 types of configuration:

G → S
G → D
S → G
S → D
D → G
D → S

Now we analyze each of them

can control, can output, able to amplify.
can control, can output, able to amplify.
can control, , unable to amplify.
can control, , able.
can't control, unable.
can't control, unable.

If the current source cannot work, the MOSFET become a resistor.
We have known a resistor can’t be used for amplification,
so the current source must be actively controlled..

Hence there’re only 3 configuration remaining, available for amplifier.
Check the small model, ( impedance relative to )

According to Thevenin’s theorem, the G→S configuration exhibits large input impedance and small output impedance. This results in higher voltage division at the input terminal and greater voltage transfer to the load. Therefore, G→S is suitable for voltage input and voltage output applications.

Similarly, G→D configuration is appropriate for voltage input and current output operation, while S→D configuration works well for current input and current output scenarios.

2.4 Common-Source Amplifier

The input is applied to gate, output is taken from D. The source is the common reference point.

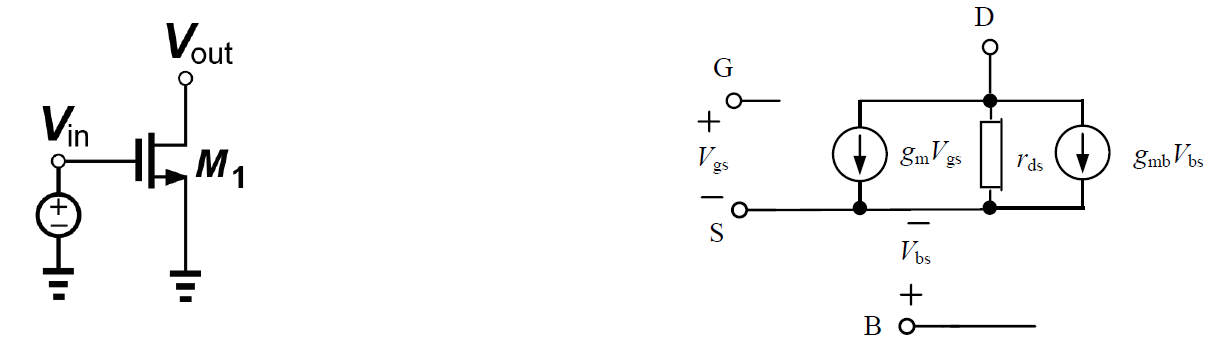
Common-Source Amplifier and AC Model

DC Analysis.

At . MOSFET cut-off, . If is float (no load).
Current on is zero. Hence .

Increase over . increases, , With rising, gradually decreases. At this time , MOSFET is in saturation.

When increases more (approaching ), there must be a time that . The MOSFET enters triode region.

DC VTC of Common Source Amplifier

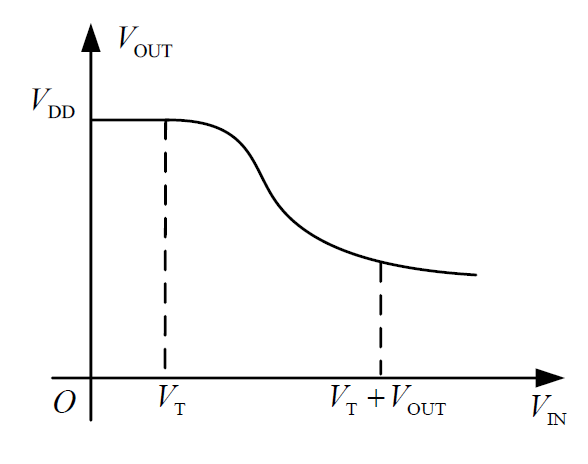
The slope reflects the intrinsic gain.

From the figure, the slope is negative, hence . Common-source amplifier is a inverse-phase amplifier.

AC Analysis

Now it comes to the small signal (AC). Replace the DC voltage sources with GND.

AC Model of Common Source

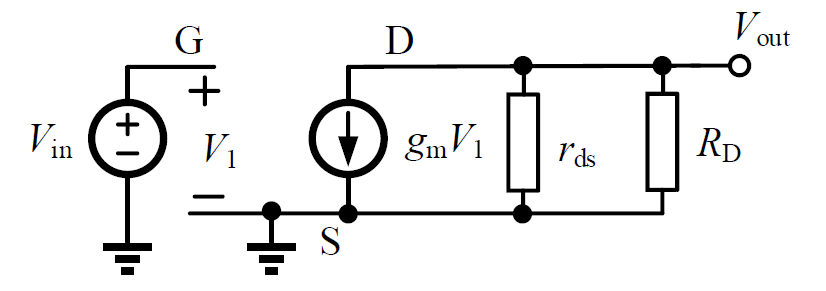
By KCL:

It gives

Also, we can also say

In practice, we assume . Apply this assumption.

To raise the gain, we can raise or . We know

Plug in

Hence to raise , we can increase , or just increase , and decrease .

But trade off is necessary here. Such optimization will bring larger device size and capacitance, causing lower speed.

If the MOSFET works in the triode region ( too large).

It has no amplification function.

Back to the saturation, since , the external resistance becomes a critical factor to limit the gain.

MOS to replace .

This MOS is configured in the triode region.

Resistance Replaced by MOSFET

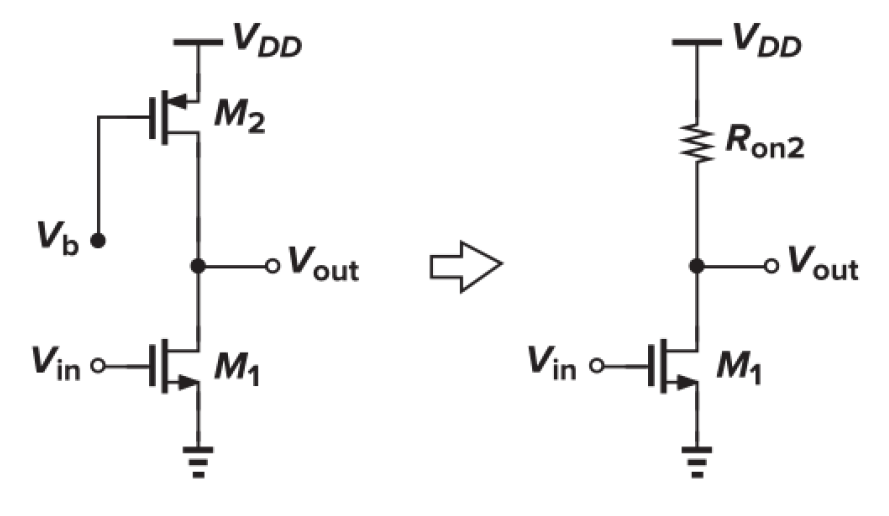
In process some parameters may drift. By using a PMOS to replace , the drift may occur together, which may cancel each other and the external property may remain unchanged.

However such cancellation is not stable. So there’s another method.

Diode Connection of MOSFET Load

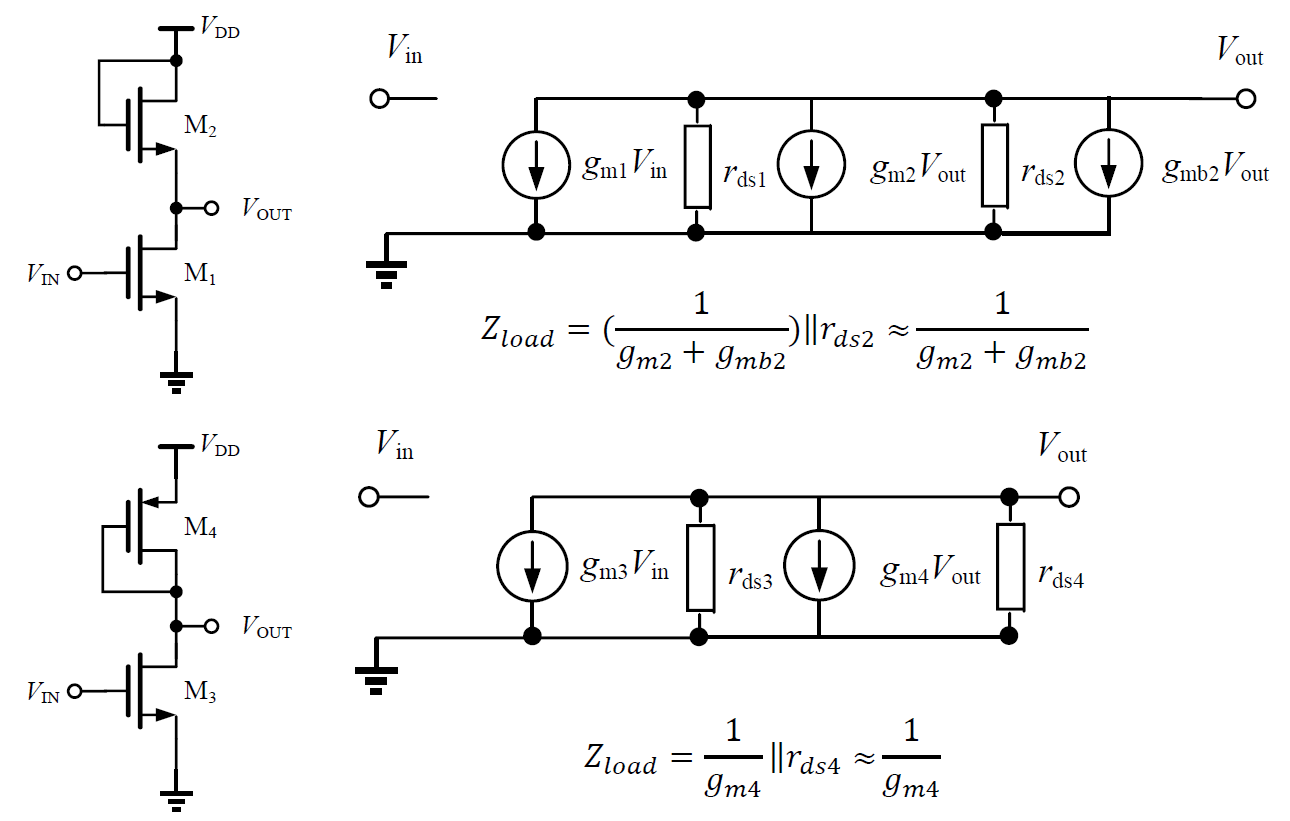
The MOS to replace is configured as “Diode connection”. In the view of source, the impedance is

Since , the MOSFET works in saturation region. The total impedance is

Gain

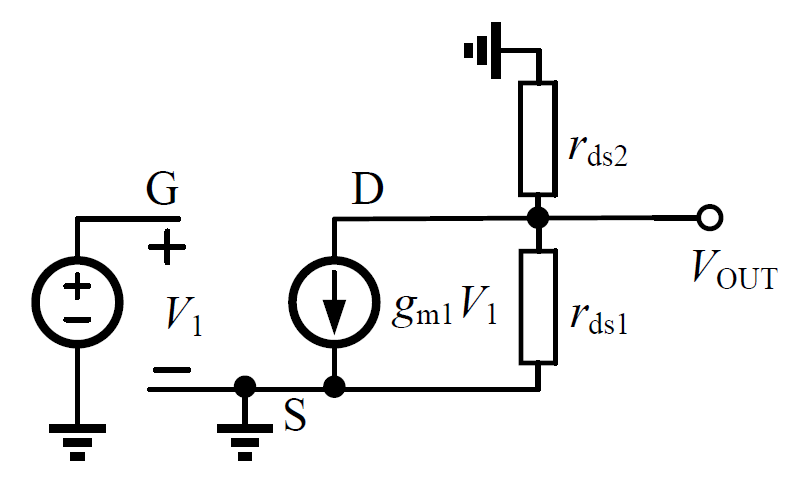
If the two MOSFETs are all NMOS, the parameter drift in process is almost the same, so they cancel better and are more precise. In fact the second NMOS serves as a DC current source. Then in AC analysis, , the current source vanishes. The total AC model is simplified to

However, for the second MOS, , so we must take into consideration.

AC Model Considering Bulk Bias

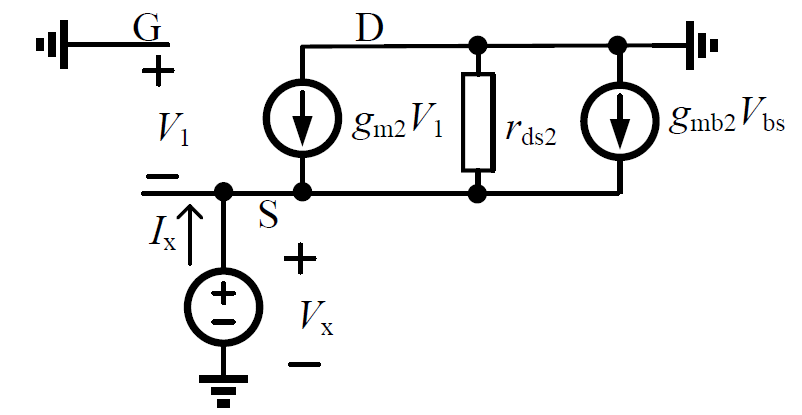
The resistance

To cancel bulk bias, use PMOS to replace NMOS

Amplifier Replaced by PMOS

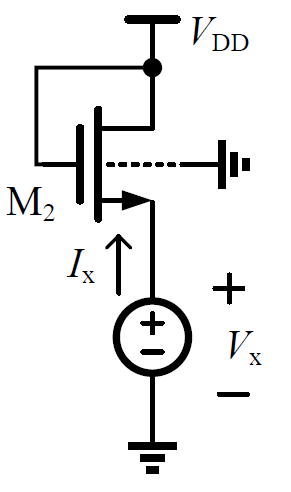
Bulk of PMOS is connected to VDD, which is the same as source.
Hence the bulk bias is cancelled.

But this circuit has some fatal problems:

Only half of the MOSFETs are used to amplify, causing a waste of current
It is sensitive to process corner (asymmetry between NMOS and PMOS)
It can only deal with a very small range of signal.

The total DC model can be plotted.

I-V Curve of Two MOSFETs

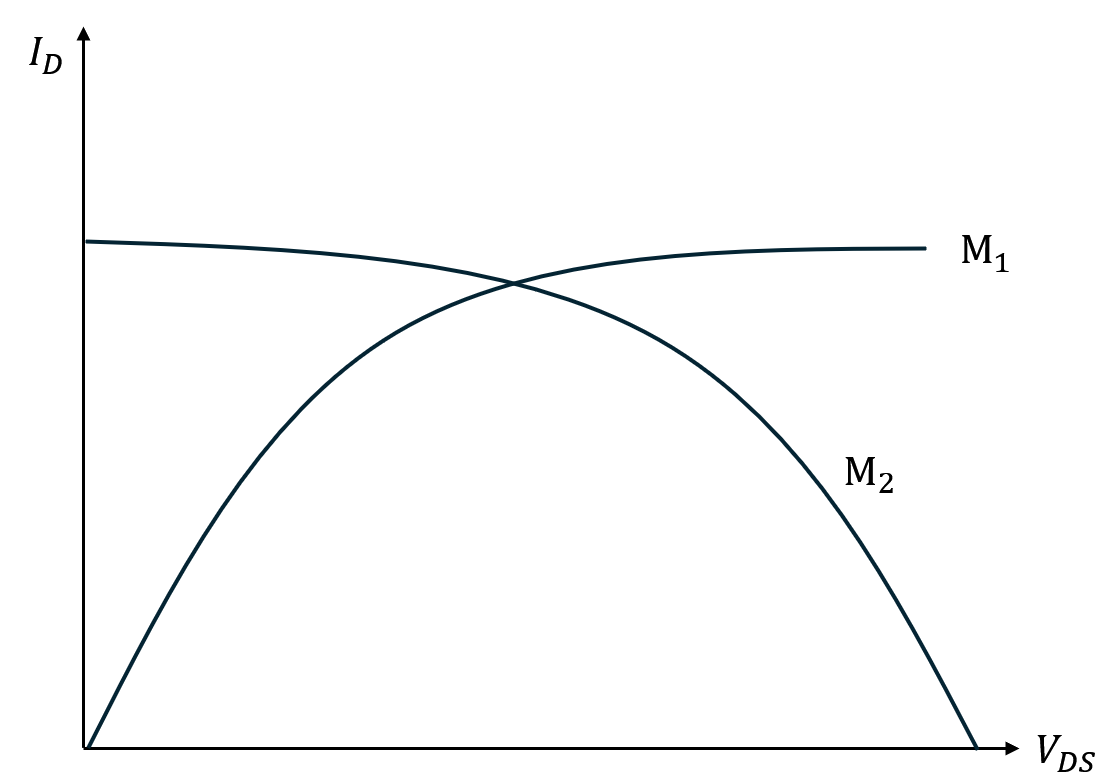
2.5 CMOS Inverter

To reduce waste, we need to place the crossing point into two saturation points. However, forcing two lines almost parallel is very difficult. In most case at least one MOSFET works in triode region.

The circuit must be changed. We connect to the terminal.

CMOS Inverter

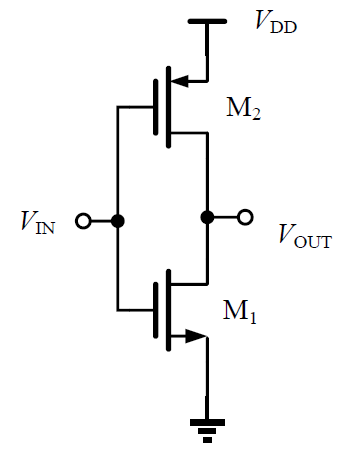
This is two amplifiers. When NMOS amplifies, PMOS serves as its load and vice versa.

In fact this is a digital inverter.
Its DC characteristic is shown below.

CMOS VTC

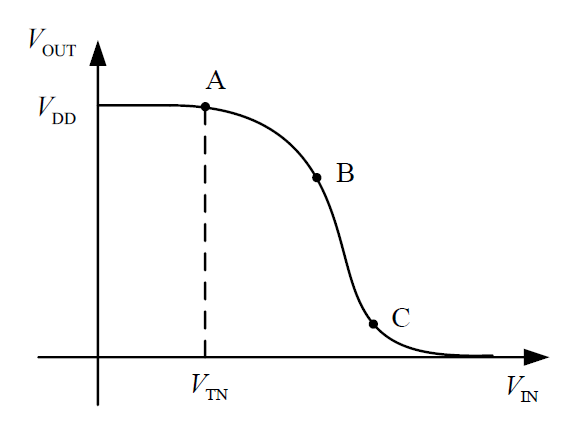
For AC model,

AC Model of CMOS Inverter

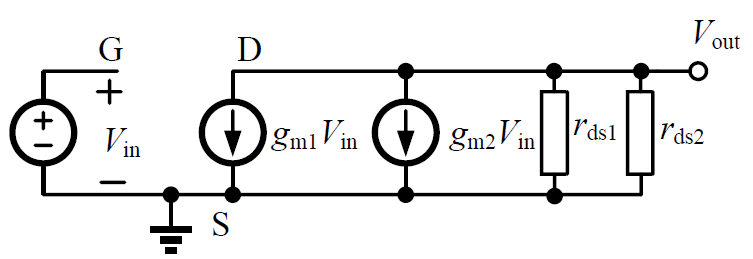
The transconductance is . The gain

With rises from 0 to VDD, NMOS changes from saturation to linear, PMOS changes from linear to saturation. Once one of the MOSFET enters triode region, decreases, causing a large decay of gain (since ).

2.6 Source Degeneration

At this time the problem of current waste is solved. But the range of double saturation is still too narrow (even narrower than before). This problem is solved by source degeneration.

Source Degeneration

AC Model of Source Degeneration

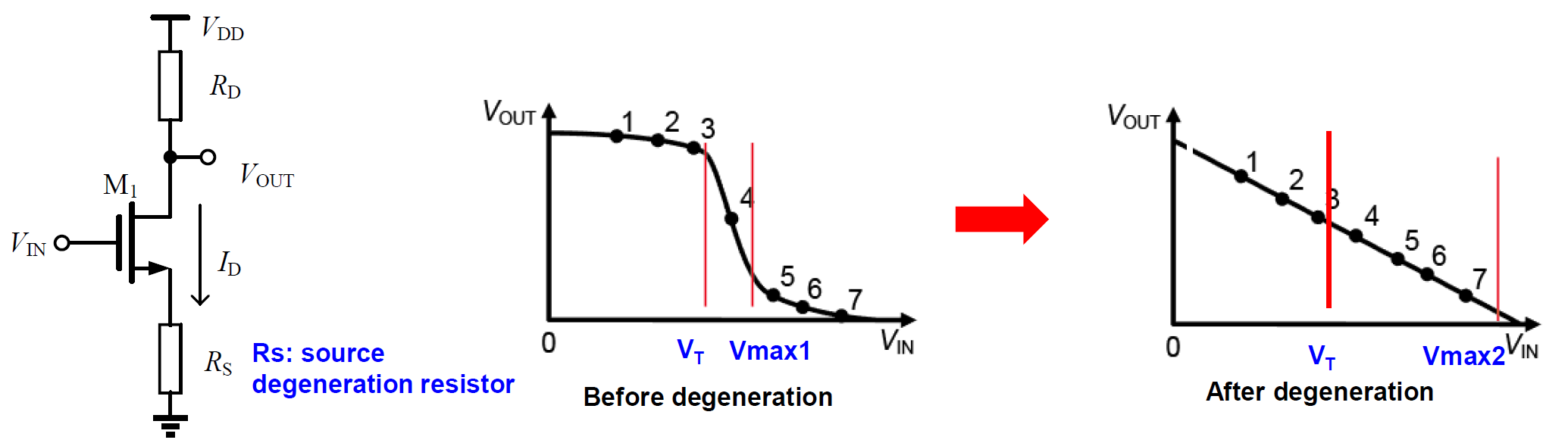
Connect D with GND, by KCL:

Eliminate :

The effective transconductance:

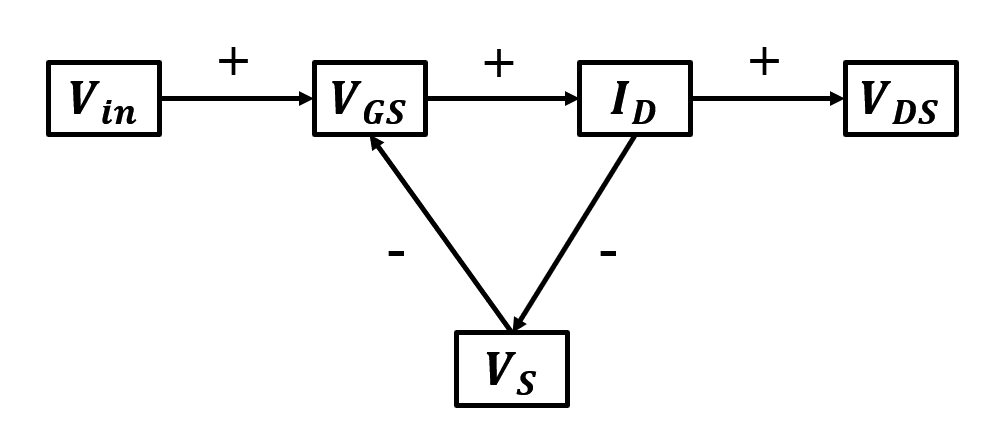
The key to widen the range of input voltage is negative feedback. Without the source resistor, when the input voltage increases, the gate-source voltage increases, leading to a rise in drain current and a drop in drain-source voltage. This makes it easy for the transistor to enter the triode region.

However, with the source resistor present, when the drain current increases, the source voltage also increases. This compensates for the variation in gate-source voltage, preventing significant changes in gate-source voltage. As a result, the drain current remains relatively stable, and the drain-source voltage also maintains stability, keeping the MOSFET in the saturation region.

Feedback Process

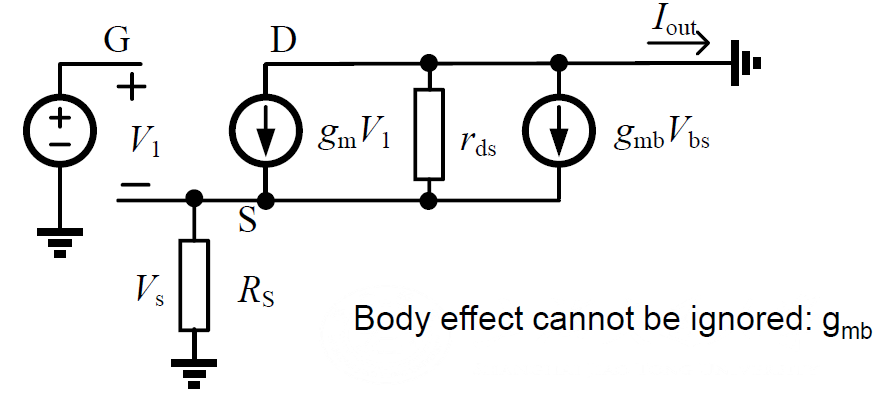
Now it comes to impedance. Apply voltage source , and connect to

Eliminate :

Finally we have the gain of common source with source degeneration:

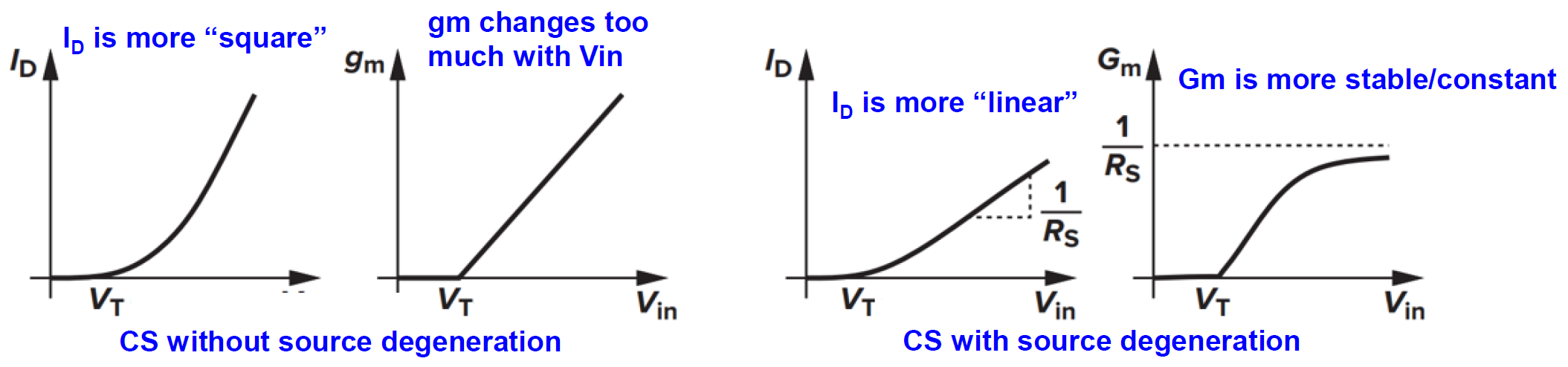
It remains constant! Source degeneration only changes the range of double saturation.

Source degeneration has other advantages. In original amplifier:

The circuit parameter is influenced by the input signal, generating new frequency components, introducing non-linear distortion, but with source degeneration:

It is independent of the input (in saturation).

Parameter w/ and w/o Source Degeneration

References:

[1] B. Razavi, Design of Analog CMOS Integrated Circuits, 2nd ed. New York, NY, USA: McGraw-Hill Education, 2017.